Required to determine if a sequence of numbers can be sorted using a stack.
A train has arrived at the cul-de-sac from track 1 (see picture). It is allowed to unhook one or several first cars from the train at once and bring them to a dead end (if you wish, you can even bring the entire train to a dead end at once). After that, take some of the wagons to the side of track 2. Then you can bring a few more wagons to the dead end, and again transport part of the wagons to the side of track 2. And so on, so that each wagon drives from track 1 to the dead end only once, and then once left the dead end on track 2. Entering the dead end from track 2 or leaving the dead end on track 1 is prohibited. You can't get from path 1 to path 2 without entering a dead end.
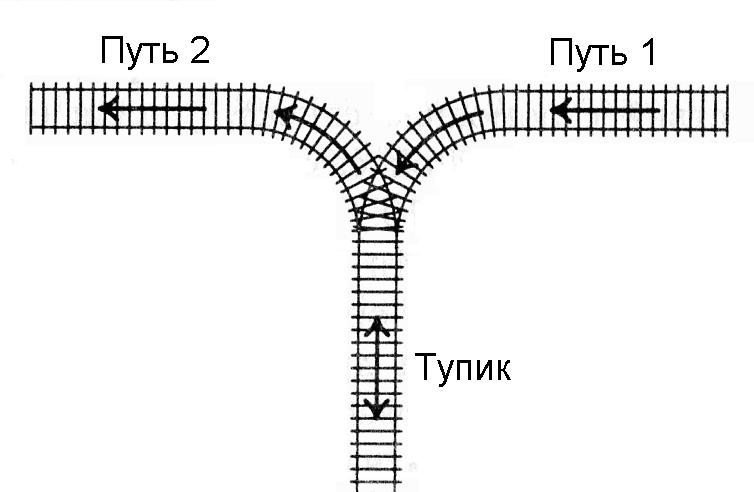
It is known in what order the train cars initially go. It is required, using the indicated operations, to make the train cars go in order (first the first, then the second, etc., counting from the head of the train traveling along track 2 away from the dead end). Write a program to determine if it can be done.
Input
Enter number N — the number of cars in the train (\(1<=N<=2000\)). Next are the car numbers in order from the head of the train traveling on track 1 towards the dead end. The cars are numbered with natural numbers from 1 to N, each of which occurs exactly once.
Output
Is it possible to make the cars go in order from 1 to N, counting from the head of the train, when the train takes track 2 from the dead end? If possible, display a message YES. If it is not possible, print NO.
Examples
| # |
Input |
Output |
Note |
| 1 |
3
3 2 1
| YES |
We need to bring the whole train to a dead end, and then take it entirely to the 2nd track |
| 2 |
4
4 1 3 2
|
YES
|
First, you need to bring two wagons to a dead end, one of which will be left in a dead end, and the second — take out to the 2nd track, then bring two more cars to the dead end and take out 3 cars standing at the dead end to the 2nd track |
| 3 |
3
2 3 1
| NO |
|