| Problem description | | Progress |
Темы:
Binary search by answer
Elementary geometry
quadtree
При игре в лапту одна команда ловит мяч и пытается осалить им бегущего. Игрок другой команды должен, перед тем как бежать, ударить мяч в поле. Известно, на какое максимальное расстояние он может ударить, а также скорости и начальные координаты игроков другой команды. Требуется выбрать направление и силу удара так, чтобы минимальное время, которое потребуется другой команде, чтобы поднять мяч с земли, было наибольшим. (Пока мяч летит, игроки стоят на местах.)
Выходные данные
Выведите сначала время, которое потребуется игрокам, чтобы добежать до мяча, а затем координаты точки, в которую нужно выбить мяч. Если таких точек несколько, выведите координаты любой из них. Время и координаты нужно вывести с точностью 10–3.
Оценка задачи
1 балл получат программы, которые верно работают, когда в поле не более двух соперников.
| Ввод |
Вывод |
|
10 2
1 1 1
-1 1 1
|
9.05539
0.00000 10.00000
|
| |
![]()
|
|
Темы:
Elementary geometry
Farmer John decided to replace the fence around his pasture.
This new fence is described by a string of characters, each of which is "N" (north), "E" (east), "S" (south), or "W" (west). Each symbol describes 1 meter of the fence. For example, if the string is NESW, this means that the fence will start one meter north, then 1 meter east, then 1 meter south, and then 1 meter west, returning to the stratum point.
The hedge always ends in the same position where it started, and it is the only point visited more than once by the hedge (and the starting point, the only point visited a second time, is at the end of the path). As a consequence, the fence encloses a single connected region of grassy pasture, even though that region may have a rather odd shape.
Farmer John wants to know if the indicated path is going clockwise or counterclockwise? Clockwise - the fenced region is on the right side of the fence, if you go along the path defined by the line. Counterclockwise - the fenced region is on the left side of the fence, if you go along the path defined by the line.
Input:
The first line contains an integer N (1≤N≤20). Each of the following N lines contains a string of at least 4 characters and at most 100 characters, describing the path of the fence.
Output:
For each of the N paths described by input, print a line containing "CW" (clockwise - clockwise) or "CCW" (counterclockwise).
Examples
| # |
Input |
Output |
Explanation |
| 1 |
2
NESW
WSSSEENWNEESSENNNNWWWS |
CW
CCW |
Both paths (? space character) denotes a starting point:
*>*
^v
<*
*<*<*<*
v ^
*<
*
v ^
* *>*>* *
^ ^
* *<* * *
v ^ v ^
*>*>* *>* |
| |
![]()
|
|
Темы:
Elementary geometry
Trouble! A meteorite is approaching the city of N. People have already managed to evacuate, but damage to houses cannot be avoided. Scientists have already figured out where the meteorite will fall. You, as an employee of an insurance company, have been asked to find out the number of houses that will be affected by a meteorite fall.
Let us introduce a rectangular coordinate system on the plane. The city is a rectangle n × m . Its lower left corner is located at the point with coordinates (0, 0) , and its upper right corner at the point with coordinates ( n - 1, m - 1) . At each point with integer coordinates inside or on the border of this rectangle, there is a house. The houses in city N are small, so they can be considered dots.
It is known that the meteorite fell to the point ( x , y ) , and the radius of its impact is equal to r . Thus, all the houses of the city at a distance of no more than r from the point of impact of the meteorite will be damaged. Find the number of houses that will be damaged.
Input
The first line contains two integers n , m ( 1 ≤ n , m ≤ 500 ) — dimensions of the city N.
The second line contains three integers x , y , r ( - 500 ≤ x , y ≤ 500 ; 0 ≤ r ≤ 500 ) — coordinates of the impact point of the meteorite and the radius of damage, respectively.
Imprint
Print one number — number of damaged houses.
Note
Illustration for the test from the example: black dots indicate damaged houses, white — survivors.

Examples
| # |
Input |
Output |
| 1 |
2 3
1 2 1
| 3 |
| |
![]()
|
|
Темы:
Elementary geometry
Constructive
In 2037, a detachment of robots landed on Mars to create a research base, one of which went to collect information about the area of deployment. At the moment, due to the failure of some nodes, the robot urgently needs to return to the place of laying the future base.
The surface of Mars in the landing area can be conditionally represented as a plane with a coordinate system introduced on it, such that the base is at the point (0, 0). The robot stopped at the point (x0, y0). It can move in four directions:
x "R" — to the right, while the x-coordinate of the robot increases by 1;
x "L" — to the left, while the x-coordinate of the robot decreases by 1;
x "U" — up, while the y-coordinate of the robot increases by 1;
x "D" — down, while the y-coordinate of the robot decreases by 1.
Due to a malfunction, the robot cannot make two consecutive movements in the same direction.
Help the robot return to base. The robot must make no more than 10,000 movements, otherwise it is discharged and will not reach the base!
Input
The only line of the input contains two integers x0 and y0 — initial coordinates of the robot (−1000 ≤ x0, y0 ≤ 1000).
Imprint
In the first line print an integer not greater than 10000 — the number of operations that the robot must do. In the second line print the operations themselves. Each operation is defined by a single letter:
right — "R" left — "L", up — "U", down — "D" Characters must be printed without spaces between them.
Examples
| # |
Input |
Output |
| 1 |
2 1 |
5
DLULD |
Remark
You are not required to output the shortest route. For example, in the above example, the shortest
the route consists of 3 movements: left, down, left.
Example test illustration:
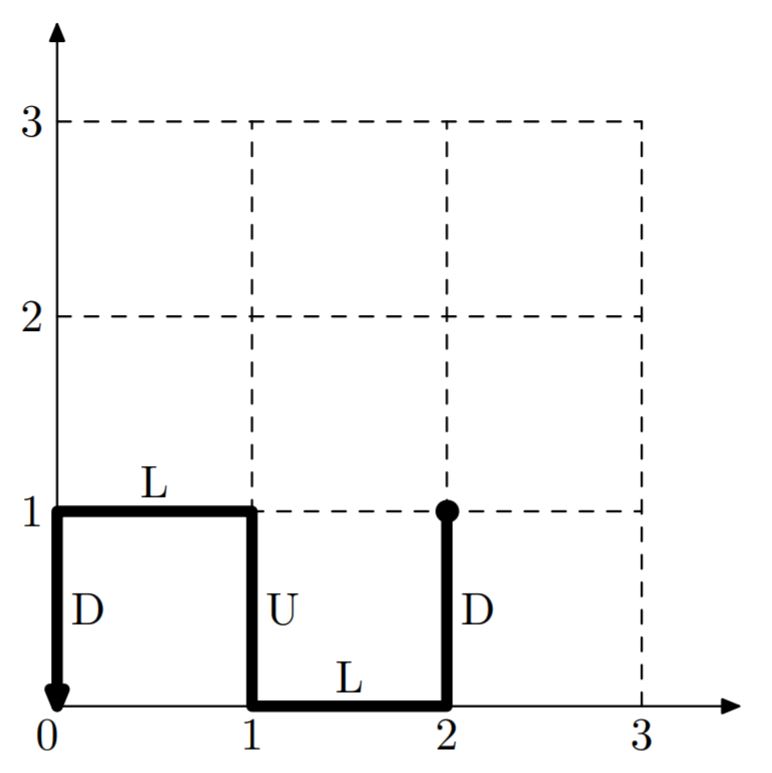
| |
![]()
|
|
Темы:
Elementary geometry
An isosceles right triangle ABC with leg length d and point X are located on the coordinate plane. The legs of the triangle lie on the coordinate axes, and the vertices are located at points: A (0,0), B (d,0), C (0,d).
Write a program that determines the relative position of the point X and the triangle. If the point X is located inside or on the sides of the triangle, print 0. If the point is outside the triangle, print the number of the vertex closest to it.
Input
First, a natural number d (not exceeding 1000) is entered, and then the coordinates of the point X – two integers from –1000 to 1000.
Imprint
If the point lies inside, on the side of the triangle, or coincides with one of the vertices, then print the number 0. If the point lies outside the triangle, then print the number of the vertex of the triangle to which it is closest (1 – to vertex A, 2 – to B, 3 to C). If a point is located at the same distance from two vertices, print the vertex with the lower number.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
5
1 1
| 0 |
The point lies inside the triangle. |
| 2 |
3
-1 -1 |
1 |
The point lies outside the triangle and vertex A is closest to it |
| 3 |
4
4 4 |
2 |
The point lies at an equal distance from vertices B and C, in this case, you need to print the vertex with the lower number, i.e. the number 2 should be displayed |
| 4 |
4
2 2 |
0 |
The point lies on the side of the triangle. |
| |
![]()
|
|
Темы:
Elementary geometry
The new metro station, which is scheduled to open at the end of this year, will have N escalators (the escalators are numbered consecutively from 1 to N). The escalators have a length L and are located at a distance H from each other. We will neglect the width of the escalator. Between each two adjacent escalators (exactly in the middle) a row of lamps will be installed. There will be K lamps in a row. Lamps are installed according to the following principle: the entire length of the escalator L is divided into K equal segments and a lamp is installed in the middle of each segment (see figure). A total of (N–1)*K lamps will be installed.
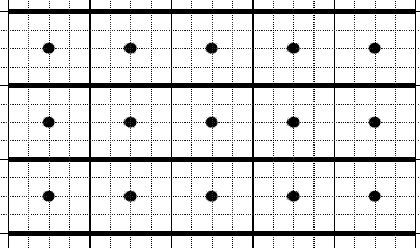
In the above figure, N=4 (escalators are shown in bold <horizontal lines), L=20, H=4, K=5.
Vasya managed to get into this station even before it opened, and even ride the escalator. He chose escalator number J. Calculate how many points on the escalator (including its beginning and end) Vasya will not see all the lamps (because other lamps will block them).
Input
The input file contains numbers N, L, H, K, J. All numbers — natural. 2≤N≤35, 1≤L≤1000, 1≤H≤1000, 1≤K≤35, 1≤J≤N.
Imprint
In the output file print a single number — task response.
Examples
| # |
Input |
Output |
| 1 |
2 20 4 5 1 |
0 |
| 2 |
4 20 4 5 2 |
11 |
| |
![]()
|
|
Темы:
Elementary geometry
Clearing — this is such a straight line that passes through the forest (that is, there are trees both on one side of this line and on the other), and at the same time it does not pass through any of the trees of the forest, and also does not touch the trees. We will say that the forest is dense if there is not a single clearing in it.
On the plan of the forest, all trees are depicted as circles. No two circles intersect or touch each other. According to this plan, it is required to determine whether the forest is dense.
Input
The input file contains first an integer N — number of trees (1?N?200). Then comes N triples of numbers that define the trees. The first two numbers set the coordinates of the center, and the third — radius. All data are specified exactly and expressed as real numbers with no more than 2 decimal places, modulo not exceeding 1000.
Imprint
The first line of the output file should contain the message YES if the forest is dense, and NO otherwise. In the second case, the second line of the output file must contain the coordinates of two points through which the clearing passes. All coordinates must be output with eight decimal places, coordinates must not exceed 2000, and the distance between the output points must be at least 100.
Examples
| # |
Input |
Output |
| 1 |
3
0.00 30.00 25.00
0.00 -30.00 25.00
40.00 0.00 16.00 |
NO
-833.3333340000 -552.7707973875
833.3333340000 552.7707973875 |
| 2 |
3
0.00 30.00 29.00
0.00 -30.00 29.00
40.00 0.00 19.00
| YES |
| |
![]()
|
|
Темы:
Elementary geometry
Finding a treasure buried by pirates is easy: all you need is – this is a map. As you know, pirates usually draw maps by hand and describe the algorithm for finding the treasure as follows: “Stand near a lonely palm tree. Walk thirty steps towards the forest, then seventeen steps towards the lake, …, finally ten steps towards the large boulder. The treasure is under it. Most of these directions simply come down to walking a certain number of steps in one of eight directions (1 – north, 2 – northeast, 3 – east, 4 – southeast, 5 – south, 6 &ndash ; southwest, 7 – west, 8 – northwest) (see fig.). The stride length in any direction is 1.
Traveling along this path is usually a great way to see the surroundings, but in this time of constant rush, no one has time for this. Therefore, treasure hunters want to go directly to the point where the treasure is buried. For example, instead of walking three steps north, one step east, one step north, three steps east, two steps south, and one step west, one can walk directly using about 3.6 steps (see pic) .
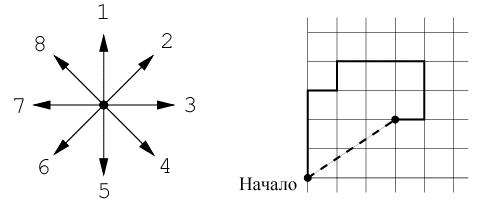
You need to write a program that, according to the instructions of the pirates, determines the point where the treasure is buried.
Input data format
First line contains the number N – number of indications (1≤N≤40). The next N lines contain the – the direction number (an integer from 1 to 8) and the number of steps (an integer from 1 to 1000). Numbers are separated by spaces.
Output data format
Print the X and Y coordinates of the point (two real numbers separated by a space) where the treasure is buried, assuming that the Ox axis is directed to the east and the Oy axis – on North. At the beginning, the treasure hunter must stand at the origin. The coordinates must be displayed with an error of no more than 10-3.
Examples
| # |
Input |
Output |
| 1 |
6
1 3
3 1
1 1
3 3
5 2
7 1
| 3.000 2.000 |
| 2 |
1
8 10
| -7.071 7.071 |
| |
![]()
|
|
Темы:
Elementary geometry
GCD and Euclid's algorithm
A polygon (not necessarily convex) on a plane is given by the coordinates of its vertices. It is required to count the number of points with integer coordinates lying inside it (but not on its border).
Input data format
The first line contains N (3 ≤N ≤1000) – the number of vertices of the polygon. The next N lines contain the coordinates (Xi, Yi) of the polygon vertices in clockwise order. Xi and Yi are integers, modulo not exceeding 1000000.
Output data format
Output a single number – desired number of points.
Examples
| # |
Input |
Output |
| 1 |
4
-1 -1
-1 1
1 1
1-1 |
1 |
| 2 |
3
0 0
0 2
20
|
0 |
| |
![]()
|
|
Темы:
Elementary geometry
At the geometry lesson, seventh-graders Vasya and Petya learned what a parallelogram is. At recess after the lesson, they began to play a game: Petya named the coordinates of four points in random order, and Vasya had to answer whether these points were the vertices of a parallelogram.
Vasya, to be honest, did not really understand the topic of parallelograms, and he needs a program that can correctly answer Petya's questions.
Recall that a parallelogram is a non-degenerate quadrilateral whose opposite sides are parallel.
Input
The first line of the input file contains an integer N (1 ≤ N ≤ 10) - the number of questions asked by Petya. Each of the next N lines contains a description of four points - four pairs of integers X and Y (−100 ≤ X ≤ 100, −100 &le ; Y ≤ 100) representing the coordinates of the point.
Imprint
For each question, determine if the given points form a parallelogram. If they form a parallelogram, then print the numbers of these points on one line separated by a space in the order of going around the parallelogram. You can start bypassing from any of the vertices. If they don't form a parallelogram, print the single number 0 on this line. The answer to each of the queries should be on a separate line.
Examples
| # |
Input |
Output |
| 1 |
3
1 1 4 2 3 0 2 3
1 1 5 2 2 3 3 0
0 0 5 1 6 3 1 2
| 1 3 2 4
0
1 2 3 4
|
| |
![]()
|
|
Темы:
Elementary geometry
Input
Four numbers – coordinates of two different points on the line.
Imprint
Three numbers – coefficients A, B and C of the equation of this line.
Examples
| # |
Input |
Output |
| 1 |
1 0 2 1 |
1 -1 -1 |
| |
![]()
|
|
Темы:
Elementary geometry
Input
Four numbers – coordinates of a point on a line and coordinates of the normal vector to this line.
Imprint
Three numbers – coefficients A, B and C of the equation of this line.
Examples
| # |
Input |
Output |
| 1 |
0 0 1 1 |
1 1 0 |
| |
![]()
|
|
Темы:
Elementary geometry
Input
Five numbers – point coordinates and coefficients A, B and C of the equation of a straight line.
Imprint
One line “YES” if the point belongs to a line, and “NO” otherwise.
Examples
| # |
Input |
Output |
| 1 |
8 7 2 -3 5 |
YES |
| |
![]()
|
|
Темы:
Elementary geometry
Input
Five numbers – point coordinates and coefficients A, B and C of the equation of a straight line.
Imprint
One number – distance from a point to a line.
Examples
| # |
Input |
Output |
| 1 |
1 5 0 -4 8 |
3.00000 |
| |
![]()
|
|
Темы:
Elementary geometry
Input
Six numbers – coordinates of the point and coordinates of the beginning and end of the vector.
Imprint
One number – distance from a point to a ray defined by a vector.
Examples
| # |
Input |
Output |
| 1 |
2 3 0 0 4 0 |
3.00000 |
| 2 |
-1 1 0 0 4 0 |
1.41421 |
| |
![]()
|
|
Темы:
Elementary geometry
Input
Six numbers – coordinates of the point and coordinates of the ends of the segment.
Imprint
One number – distance from a point to a segment.
Examples
| # |
Input |
Output |
| 1 |
0 0 0 0 4 0 |
0.00000 |
| 2 |
4 0 0 0 4 0 |
0.00000 |
| |
![]()
|
|
Темы:
Elementary geometry
Input
Eight numbers – coordinates of the ends of two segments.
Imprint
One line “YES” if the segments have common points, and “NO” otherwise.
Examples
| # |
Input |
Output |
| 1 |
1 2 1 2
1 2 1 2
| YES |
| 2 |
3 3 5 6
5 6 3 3
| YES |
| |
![]()
|
|
Темы:
Elementary geometry
Input
Six numbers – coefficients A, B and C of the normal equation of two different non-parallel lines (first for one line, then for the other).
Imprint
Two numbers – coordinates of the point of their intersection.
Examples
| # |
Input |
Output |
| 1 |
4 -4 0 0 -3 6 |
2.00000 2.00000 |
| |
![]()
|
|
Темы:
Elementary geometry
Input
Six numbers – coordinates of points X, Y and Z.
Imprint
Three numbers – coefficients of the equation of the angle bisector YXZ.
Examples
| # |
Input |
Output |
| 1 |
0 0 1 0 0 1 |
1.000000 -1.000000 0.000000 |
| 2 |
0 0 1 3 1 -3 |
0.000000 -0.632456 0.000000 |
| |
![]()
|
|
Темы:
Elementary geometry
Input
Five numbers – coordinates of the center and radius of the circle, coordinates of the point.
Imprint
The first line contains one number K, equal to the number of points of intersection of the tangents to the circle from the given point with the circle itself. Next in K lines are the coordinates of the points themselves.
Examples
| # |
Input |
Output |
| 1 |
2 2 2 2 5 |
2
0.50929 3.33333
3.49071 3.33333 |
| |
![]()
|
|
Темы:
Elementary geometry
Input
Six numbers – the coordinates of the center and the radius of the circle and the coefficients A, B and C of the normal equation of the line.
Imprint
The first line contains one number K, equal to the number of points of intersection of the line with the circle. Next in K lines are the coordinates of the points themselves.
Examples
| # |
Input |
Output |
| 1 |
2 3 1 1 -1 0 |
2
3.00000 3.00000
2.00000 2.00000
|
| |
![]()
|
|
Темы:
Elementary geometry
Input
Six numbers – the coordinates of the center and the radii of the two circles.
Imprint
If the number of common points of the circles is finite, in the first line print one number K, equal to this number, then in K lines the coordinates of the points themselves. If there are infinitely many specified points, output a single number “3”.
Examples
| # |
Input |
Output |
| 1 |
3 4 5 11 4 2 |
0 |
| 2 |
3 4 5 9 4 2 |
2
7.75000 5.56125
7.75000 2.43875 |
| |
![]()
|
|
Темы:
Elementary geometry
Input
Seven numbers – coordinates of the center and radius of a circle (possibly degenerate) and real coordinates of two points on it, up to the fifth decimal place.
Imprint
One number – the length of the smaller arc of the circle enclosed between the specified points.
Examples
| # |
Input |
Output |
| 1 |
0 0 1 0 1 1 0 |
1.57080 |
| |
![]()
|
|
Темы:
structures
Using sort
Elementary geometry
Print all initial points in ascending order of their distances from the origin.
Create a Point structure and store the original data in an array of Point structures.
Input
The program receives a set of points on the plane as input. First, the number of points n is given, then there is a sequence of n lines, each of which contains two numbers: the coordinates of the point. The value of n does not exceed 100, all initial coordinates – integers not exceeding 103.
Imprint
It is necessary to display all initial points in ascending order of their distances from the origin. The program displays only the coordinates of the points, there is no need to display their number.
Examples
| # |
Input |
Output |
| 1 |
2
1 2
2 3
| 1 2
2 3
|
| |
![]()
|
|
Темы:
Dynamic Table Programming
Elementary geometry
Algorithms on graphs
Santa Claus must visit N cities overnight. He has a two-dimensional plan for the location of all cities. The plan is drawn in Cartesian system of coordinates, in which point (0, 0) indicates the place where Father Frost starts. Each city on the plan is marked with a point with the coordinate ;(Xi, Yi). Also on the map are marked M points with coordinates (Pi, Qi) , in which accelerators are located. In order to have time to deliver all the gifts, Santa Claus can use an accelerator that doubles his speed (or maybe not use it).
On New Year's Eve Santa Claus starts from the starting point, visits all N cities and returns.
Father Frost's initial speed is 1. Find the shortest time it takes for Santa Claus to visit all the cities and return back. We will neglect the time at which he lays out all the gifts!
Input
The first line of the input contains two integers N and M (1 <= N <= 12, 0 <= M <=5). The following N lines contain the coordinates of cities (Xi, Yi). Then there are M lines with accelerator coordinates (Pi, Qi). All coordinates are different and there is no (0, 0).
Imprint
Print the answer to the problem, with an accuracy of at least 6 decimal places.
Examples
| # |
Input |
Output |
Note |
| 1 |
2 1
1 1
0 1
10 |
2 1
1 1
0 1
10 |
Here is one of the best ways to distribute all the gifts
- Move distance 1 from the origin to accelerator 1 at speed 1, spending time 1.
- Move distance 1 from accelerator 1 to city 1 at speed 2 in time 0.5.
- Travel distance 1 from city 1 to city 2 at speed 2, taking time 0.5.
- Travel distance 1 from city 2 to origin at speed 2 in time 0.5.
|
| 2 |
2 1
1 1
0 1
1000 |
3.4142135624 |
Here is one of the best ways to distribute all the gifts
- Travel distance 1.41... from origin to city 1 at speed 1, spending time 1.41....
- Travel distance 1 from city 1 to city 2 at speed 1, spending time 1.
- Travel distance 1 from city 2 to the origin at speed 1, spending time 1.
|
| 3 |
1 2
4 4
10
0 1
| 4.3713203436 |
Here is one of the best ways to distribute all the gifts
- Move distance 1 from the origin to accelerator 1 at speed 1, spending time 1.
- Move distance 1.41... from accelerator 1 to accelerator 2 at speed 2, spending time 0.707....
- Move distance 5 from accelerator 2 to city 1 at speed 4 in time 1.25.
- Travel distance 5.65... from city 1 to origin at speed 4, spending time 1.41....
|
| |
![]()
|