| Problem description | | Progress |
|
Темы:
Elementary geometry
Constructive
In 2037, a detachment of robots landed on Mars to create a research base, one of which went to collect information about the area of deployment. At the moment, due to the failure of some nodes, the robot urgently needs to return to the place of laying the future base.
The surface of Mars in the landing area can be conditionally represented as a plane with a coordinate system introduced on it, such that the base is at the point (0, 0). The robot stopped at the point (x0, y0). It can move in four directions:
x "R" — to the right, while the x-coordinate of the robot increases by 1;
x "L" — to the left, while the x-coordinate of the robot decreases by 1;
x "U" — up, while the y-coordinate of the robot increases by 1;
x "D" — down, while the y-coordinate of the robot decreases by 1.
Due to a malfunction, the robot cannot make two consecutive movements in the same direction.
Help the robot return to base. The robot must make no more than 10,000 movements, otherwise it is discharged and will not reach the base!
Input
The only line of the input contains two integers x0 and y0 — initial coordinates of the robot (−1000 ≤ x0, y0 ≤ 1000).
Imprint
In the first line print an integer not greater than 10000 — the number of operations that the robot must do. In the second line print the operations themselves. Each operation is defined by a single letter:
right — "R" left — "L", up — "U", down — "D" Characters must be printed without spaces between them.
Examples
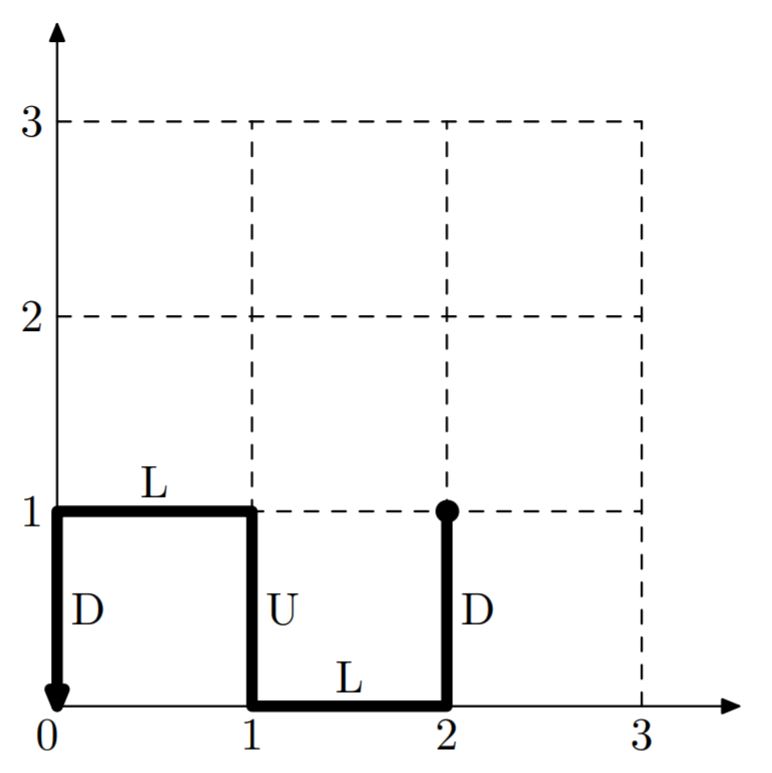
| # |
Input |
Output |
| 1 |
2 1 |
5
DLULD |
Remark
You are not required to output the shortest route. For example, in the above example, the shortest
the route consists of 3 movements: left, down, left.
Example test illustration:
| |
![]()
|
|
Темы:
Strings
Constructive
Given three strings consisting of lowercase Latin letters. With these strings, you can perform the following operations: either replace one character of the string with two of the same characters (for example, replace the character "a" with "aa"), or, conversely, replace two consecutive identical characters with one of the same character.
It is necessary to use these operations to make all three strings equal to some other common string S, or to determine that it is impossible to do so. At the same time, it is necessary to minimize the total number of operations.
Input
The program receives as input three strings consisting of lowercase Latin letters. The length of each line does not exceed 100 characters.
Imprint
If it is possible to make all three strings equal using the indicated operations, print a string S such that the total number of operations required to convert all three given strings to the string S will be minimal. If this cannot be done, the program should print a single word IMPOSSIBLE (in capital letters).
Examples
| # |
Input |
Output |
| 1 |
aaaza
aazzaa
azzza |
aazza |
| 2 |
xy
yx |
IMPOSSIBLE |
| |
![]()
|
|
Темы:
Constructive
Let's call a palindrome a non-empty string that reads the same from right to left and from left to right. For example, " abcba "," a " and « abba » are palindromes, and " abab » and « xy » are not.
Let's call a substring of a string a string obtained by discarding some (possibly zero) number of characters from the beginning and from the end of the string. For example, " abc "," ab » and « c » are substrings of the string « abc ", and « ac » and « d » are not.
Let's call the palindromicity of a string the number of its substrings that are palindromes. For example, the palindromic string « aaa " is 6, since all its substrings are palindromes, and the palindromicity of the string « abc " is 3 because only substrings of length 1 are palindromes.
You are given a string s. You can arbitrarily rearrange the characters in it. It is required to get a string that has the maximum palindromicity.
Input
The first line contains an integer n (1 ≤ n ≤ 100000) — string length s.
The second line contains a string s, consisting of n lowercase Latin letters.
Imprint
Output a string t that consists of the same characters (including multiplicities) as s and has the maximum palindromicity among all strings that can be obtained from s by permuting characters.
If there are several matching lines, print any one.
Note
In the first example, the string « ololo " there are 9 palindrome substrings: « o "," l "," o "," l "," o "," olo "," lol "," olo "," ololo ". Note that some substrings match but are counted multiple times.
In the second example, the palindromicity of the string « abccbaghghghgdfd » is 29.
Examples
| # |
Input |
Output |
| 1 |
5
oolol |
ololo |
| 2 |
16
gagadbcgghhchbdf |
abccbaghghghgdfd |
| |
![]()
|
|
Темы:
Constructive
There are N cities on the east-west line. Cities are numbered from 1 to N in order from west to east. Each point on the line has one-dimensional coordinates, and the point further east has the larger coordinate value. City coordinate i - Xi. You are in city 1 and want to visit all other cities. You have two ways to travel:
- Walk along the line. Your fatigue level increases by A each time you travel a distance of 1, regardless of direction.
- Teleport to any location of your choice. Your fatigue level increases by B regardless of the distance traveled.
Find the lowest possible total increase in your fatigue level when you visit all the cities in these two ways.
Input
The first line contains three integers N (\(2<=N<=10^5\)), A< /code> (\(1<=A<=10^9\)), B (\(1<=B<=10^9\)). The second line contains the coordinates of cities Xi (\(1<=X_i<=10^9\) ), for all i \(X_i <X_{i+1}\)( \(1<=i<=N-1\)).
Imprint
Display the answer to the problem.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
4 2 5
1 2 5 7
| 11 |
From city 1, travel distance 1 to city 2, then teleport to city 3, then travel distance 2 to city 4.
The total increase in your fatigue level in this case is 2 x; 1 + 5 + 2 x 2 = 11, which is the smallest possible value. |
| 2 |
7 1 100
40 43 45 105 108 115 124
| 84 |
From city 1, walk to city 7.
The total increase in your fatigue level in this case is 84, which is the lowest possible value. |
| 3 |
7 1 2
24 35 40 68 72 99 103
| 12 |
Visit all cities in any order by teleporting six times.
The total increase in fatigue level in this case is 12, which is the lowest possible value. |
| |
![]()
|
|
Темы:
Constructive
Wushan decided to play with a six-sided die. Each of the six sides has an integer from 1 to 6, and the two numbers on opposite sides always add up to 7. Wushan first places the die on the table with a random side up, and then repeats the next operation. Rotate the die by 90 ° in one of the following directions: left, right, forward (the cube will move closer), and back (the cube will move further), then get y points, where y is the number written in side facing up.
For example, let's consider the situation where the side showing 1 is facing up, the near side is showing 5, and the right side is showing 4, as shown in the figure (original position for our example).
If the cube is turned to the right, as shown in the figure, the side showing 3 will be facing up. If the cube is rotated to the left from its original position, the side showing 4 will look up. The side showing 2 will be at the top if the cube is turned forward from its original position, and the side showing 5 will be facing up if the cube is rotated back from its original position.
Find the minimum number of operations Wushan must perform in order to score at least x points.
Input
The input is an integer x (\(1<=x<=10^{15}\)).
Imprint
Display the answer.
Examples
| # |
Input |
Output |
| 1 |
7 |
2 |
| 2 |
149696127901 |
27217477801 |
| |
![]()
|
|
Темы:
Constructive
Count sort
Wushan decided to play a card game. He has a deck of N edible cards. The ith card has an integer Ai written on top. Wushan performs the operation described below zero or more times, so that the values written on the remaining cards will be pairwise different.
Find the maximum possible number of remaining cards. Here, N is odd, which ensures that at least one card is saved.
Operation: draw three random cards from the deck. Of these three cards, eat two: one with the highest value and the other with the lowest value. Then return the remaining one card to the deck.
Input
The first line contains an odd number N (\(3<=N<=10^5\)). The second line contains N numbers Ai (\(1<=A_i<= 10^5\))
Imprint
Output the maximum possible number of remaining cards.
Examples
| # |
Input |
Output |
Explanations |
| 1 |
5
1 2 1 3 7
| 3 |
The optimal solution is to perform the operation once, drawing two cards from 1 and one card from 2. One card from 1 and the other from 2 will be eaten, and the remaining card with 1 will be returned to the deck.
Then the values written on the remaining cards in the deck will be pairwise different: 1, 3 and 7. |
| 2 |
15
1 3 5 2 1 3 2 8 8 6 2 6 11 1 1
| 7 |
|
| |
![]()
|
|
Темы:
"Two Pointers"
Greedy Algorithm
Constructive
Tommy has a children's toy "sorter", with n pegs arranged in a row. There is now no more than one disk on each peg (that is, there is a disk on some peg, but on some it No). Tommy wants to rearrange the given disks on the pegs so that they form a non-decreasing sequence when viewed from left to right. That is, on each next peg, the number of disks must be no less than on the previous one. What is the minimum number of Tommy's disks that need to be shifted?
Please note that some pegs may be empty at the end of sorting. Some pegs may contain more than 1 disc.
Input
The program receives as input in the first line an integer n (1 <= n <= 105), the number of peg on "sorter". The next line contains n integers a1, a2, ... an – the presence of a disc on the corresponding peg (0 <= ai <= 1). the number 0 means that there is no disk on the ith peg, 1 – there is a disc.
Imprint
Print the answer to the problem.
Examples
| # |
Input |
Output |
| 1 |
8
0 0 1 1 1 1 1 1
|
0
|
| 2 |
eleven
1 1 0 0 1 0 0 1 1 1 0
|
3
|
| |
![]()
|