| Problem description | | Progress |
|
Темы:
Formula derivation
Two integers are entered from the keyboard - the sides of the rectangle. Write a program to find its perimeter and the length of the diagonal. Print the perimeter of the rectangle in the first line, and the length of its diagonal in the second line.
Example
| # |
Input |
Output |
| 1 |
2 13 |
30
13.152946 |
| |
![]()
|
|
Темы:
Formula derivation
Whole numbers
King wants to become a baker and lead a simple lifestyle.
The royal kitchen is covered with a kitchen apron, which is divided into squares with side A see. King wants to hang a picture of his family on the apron. He knows the point at which the lower left corner of the painting is in contact, as well as the width and height of the painting itself. And then he wanted to know the number of squares that would be partially or completely covered by the picture.
Input format
The first line contains the number A - the side of one square of the kitchen apron.
The second and third lines - the numbers X and Y - are the coordinates of the lower left corner of the picture.
The fourth and fifth lines - the numbers W and H - the width and height of the picture.
The axis OX is directed to the right, the axis OY is directed up.
The lower left corner of one of the squares of the kitchen apron is at the origin. All numbers are integers not exceeding 2 × 109, numbers A, W, H are positive, numbers X and Y are positive or equal to 0.
Output format
Output one number - the number of tiles completely or partially covered by the picture.
A square is considered a closed picture if the intersection of the picture and the square has a non-zero area, that is, touching the picture and the square is not considered overlapping.
Example
|
№
|
Input |
Output |
|
1
|
10
15
5
35
20
|
12
|
Description
Side of the square (side of the cell in the figure) A = 10.
The lower left corner of the picture has coordinates (15, 5), the picture has a width of 35 cm and a height of 20 cm.
The painting completely or partially covers 12 squares

| |
![]()
|
|
Темы:
Formula derivation
Whole numbers
В школе № 2007 на уроке информатики в системе SilverTests Васе попалась следующая задача: «В младшей группе одного объединённого детского сада воспитательница изучала с детишками порядок цветов радуги. Она отыскала семь соответствующих цветных мелков и начала рисовать полоски, не нарушая последовательности цветов. Начала она с красной полоски. Когда доходила до фиолетовой полоски, опять рисовала красную. Воспитательница успела нарисовать N полосок, когда у неё закончились мелки. Напишите программу, которая вычисляет количество полосок каждого цвета». Вася взялся писать программу, но тут обнаружилось, что на клавиатуре отсутствует клавиша с буквой «i». Помогите Васе написать программу с учётом этого обстоятельства.
Входные данные: Вводится одно целое положительное число N > 0.
Выходные данные: Выведите ответ на задачу.
Если в коде программы встречается буква «i» система выдаст сообщение: Использование запрещенных операторов
Примеры
| № |
Входные данные |
Выходные данные |
| 1 |
3 |
'red - 1'
'orange - 1'
'yellow - 1'
'green - 0'
'blue - 0'
'sky - 0'
'purple - 0' |
| |
![]()
|
|
Темы:
Formula derivation
The program receives two integers n, m, each in a separate line \(0<n<=12, 0< =m<60\) , indicating a point in time "n hours m minutes". Determine the smallest number of full minutes that must elapse before the hour and minute hands on the dial coincide, not necessarily at some division. Do not use real arithmetic.
The task must be solved without using conditional operators (including without the ternary operator ?: in C++) and/or loops. In addition, you cannot use comparison operations and the logical (boolean) data type.
Examples
| # |
Input |
Output |
| 1 |
2
50 |
26 |
| 2 |
3
0 |
16 |
| |
![]()
|
|
Темы:
Formula derivation
Conditional operator
Peter needs to get from floor A to floor B. To call the elevator on all floors of the office building, except for the first and last, there are two buttons – to move down and move up. At the moment when Peter pressed the desired call button, the elevator was on floor C and carried one passenger to floor D. If the elevator passes the floor on which the call button is pressed, and the elevator moves in the appropriate direction, then the elevator stops to put an additional passenger. The elevator moves between adjacent floors in one unit of time, and it also takes one unit of time for the elevator to stop on the floor for disembarking or boarding passengers.
Write a program to calculate how long it will take Peter to reach floor B, assuming no one else calls the elevator.
The first line of input contains four integers A, B, C, and D separated by a single space (1 ≤ A, B, C, D ≤ 20, A≠B, C≠D, A≠C).< /div>
Output one integer – the number of time units from the moment the elevator is called to the moment when Peter exits the elevator on floor B.
| Input |
Output |
| 3 9 2 5 |
10 |
| 3 9 5 2 |
13 |
Note:
Explanation for example 1
The elevator will reach the 3rd floor in 1 unit of time, stop for 1 unit of time for Peter to get into the elevator, then after 2 units of time it will reach the 5th floor and stop for 1 unit of time to disembark the previous passenger, after In 4 time units, the elevator will take Peter to the 9th floor, and after 1 time unit, Peter will exit the elevator.
| |
![]()
|
|
Темы:
Formula derivation
Two integers are entered from the keyboard - the legs of a right-angled triangle. Write a program to determine the hypotenuse of such a triangle.
Example
| # |
Input |
Output |
| 1 |
3 4 |
5.000000 |
| |
![]()
|
|
Темы:
Formula derivation
Two integers are entered from the keyboard - the legs of a right-angled triangle. Write a program to determine the perimeter of such a triangle.
Example
| # |
Input |
Output |
| 1 |
3 4 |
12.000000 |
| |
![]()
|
|
Темы:
Formula derivation
Whole numbers
On one side of the street there are houses with odd numbers (1, 3, 5, …), on the other side – with even (2, 4, 6, …). House number 1 is located opposite house number 2, & nbsp; house number 3 – opposite house number 4, etc. You need to walk one minute along the street to the neighboring house, no matter which side of the street it is on (that is, from house number 1 you need to walk one minute both to house number 3 and to house number 4). There is no need to go to the house opposite.

Gromozeka went outside from house number A and must reach house number B. Determine how many minutes he needs to walk along the street.
It is forbidden to use any algorithmic constructs to solve this problem. You can only use arithmetic operations (without using built-in functions).
Input data
The program receives as input two distinct positive integers A and B not exceeding 2×109, – house numbers.
Imprint
The program should output a single number – desired number of minutes.
Examples
| |
![]()
|
|
Темы:
Whole numbers
Formula derivation
A shoe factory is about to start producing an elite model of boots. The holes for lacing will be arranged in two rows, the distance between the rows is a, and the distance between the holes in the row b. The number of holes in each row is N. Lacing should take place in an elite way “up, horizontally to another row, up, horizontally, etc.” (see picture). In addition, in order for the laces to be tied with an elite bow, the length of the free end of the lace must be l. What is the lace length for these boots?
Forbidden to use if, while, for, repeat-until statements (Pascal)
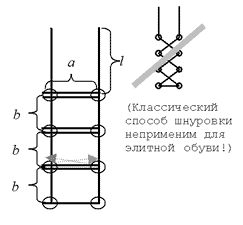
Input: The program takes as input four natural numbers a, b, l and N.
Output: The program should output a single number – desired lace length.
Examples
input
2
1
3
4
output
26
| |
![]()
|
|
Темы:
Real numbers
Formula derivation
Write a program that calculates the value of y.
\(y = \frac {-1} {x^2}\)
Input
The input is an integer x (x > 0).
Imprint
Print the value y.
Examples
| # |
Input |
Output |
| 1 |
2 |
-0.25 |
| 2 |
1 |
-1 |
| |
![]()
|
|
Темы:
Real numbers
Formula derivation
Write a program that calculates the value of y.
\(y = \frac {a + b} {2}\)
Input
The input is 2 integers a and b.
Imprint
Print the value y.
Examples
| # |
Input |
Output |
| 1 |
2 2 |
2 |
| 2 |
1 2 |
1.5 |
| |
![]()
|
|
Темы:
Formula derivation
Real numbers
Write a program that calculates the value of y.
\(y = 5.45 \cdot \frac {a + 2 \cdot b} {2-a}\)
Input
The input is 2 integers a (a>2) and b.
Imprint
Print the value y.
Examples
| # |
Input |
Output |
| 1 |
4 2 |
-21.80 |
| 2 |
1 2 |
27.25 |
| |
![]()
|
|
Темы:
Real numbers
Formula derivation
Write a program that calculates the y value.
\(y = \frac a {b \cdot c}\)
Input
The input is 3 integers a, b, c (b, c > 0).
Imprint
Output the value y.
Example
| # |
Input |
Output |
| 1 |
4 2 3 |
0.67 |
| 2 |
1 2 1 |
0.5 |
| |
![]()
|
|
Темы:
Formula derivation
Sasha doesn't like spinners at all, so he draws in his notebook. He took a notebook sheet from N × M cells and numbered all the cells with different numbers. Now he was wondering how many different rectangles he could cut from this sheet of paper along the borders of the cells.
The program receives two numbers N and M as input – dimensions of the original sheet. All numbers – positive integers not exceeding 75000.
The program should output a single number – the number of rectangles that can be cut from a given sheet of paper (the entire sheet is also considered one of the possible rectangles).
| Input |
Output |
Note |
2
2 |
9 |
 |
3
1 |
6 |
 |
| |
![]()
|
|
Темы:
Formula derivation
Scientists plan to conduct an important experiment using the research module
on planet X-2019. During the experiment, two measurements will be taken: the main and the control.
Each measurement takes exactly one hour and must start an integer number of hours after
start of the research module.
The data of the experiment is planned to be immediately transferred to the orbital station. Communication channel
with the orbital station will be installed from the l-th to the r-th hour from the start of the research module, inclusive. In addition, according to the plan of the experiment between measurements, the planet
must make an integer number of revolutions around its axis. Planet X-2019 turns around
around its axis in a hours.
Thus, if the measurements are carried out at the i-th and j-th hour, then the inequality l <= i < j <= r, and the value (j < minus; i) must be a multiple of a. Now scientists need to understand
how many different ways to take measurements.
It is required to write a program that, given the limits of the measurement time l and r and the period of revolution of the planet around its axis a, determines the number of possible ways to spend
measurements: number of pairs of integers i and j such that l <= i < j <= r and the value (j − i) is a multiple of a.
Input data format
The input contains three integers, one per line: l, r, and a (1 <= l < r <= 109,1 <= a <= 109).
Output format
Print one integer: the number of ways to measure.
|
Enter |
Output |
1
5
2 |
4 |
4
9
6 |
0 |
Explanations for examples
In the first example, you can take measurements at the following pairs of hours: (1, 3), (1, 5), (2, 4), (3, 5).
In the second example, the duration of the communication channel is not enough to spend two
measurements.
| |
![]()
|
|
Темы:
Formula derivation
The presidential elections in the United States are held indirectly. A simplified diagram looks like this. First, elections are held in constituencies, in these elections voters (that is, all citizens who have the right to vote) vote. Then the voting takes place in the Electoral College, in this election each constituency is represented by one elector who votes for the candidate who won the election in this
constituency. There are several presidential candidates, but in reality the struggle is between the two candidates from the main parties, so in order to win the election, the candidate must secure strictly more than half of the votes in the Electoral College. But in order for the elector to vote for this candidate, it is necessary that this candidate also get strictly more than half in his constituency
the votes of the electorate. There are cases (for example, in 2016) when, due to such an indirect electoral system, a candidate won the election for whom fewer voters voted than for another candidate who lost the election.
Let the electoral college consist of N people, that is, there are N electoral districts. Each electoral district, in turn, consists of K voters. Determine the smallest number of voters who could vote for the candidate who won the election.
The program receives two integers N and K as input (1 ≤ N ≤ 10 3 , 1 ≤ K ≤ 10 6 ) and should output a single integer &ndash ; desired number of voters.
|
Enter |
Output |
Note |
5
3 |
6 |
For this candidate to receive a majority in the board
electors, it is necessary that 3 out of 5 electors
voted for him, that is, the candidate must win
victory in 3 districts. Each constituency consists of 3 voters,
therefore, to win in the district, you need to get 2 votes
in this district.
|
| |
![]()
|
|
Темы:
Formula derivation
Comet Barmaley is known to be visible from Earth every C years. Curiously, this happens in years divisible by C, i.e. C, 2xC, 3xC, etc. Not everyone is destined to see this comet at least once in their life. However, there are happy centenarians who made her arrive even several times.
It is believed that for the first time this comet was seen and documented by the famous medieval astronomer Barmaleo Barmaley. In honor of him, she got her name. They say that during his long life he managed to make many great discoveries in various fields of science. However, recently historians have begun to doubt whether Barmaleo Barmalei made all the discoveries attributed to him. In particular, they were interested in how many times in his life a scientist could see a comet named after him.
Barmaleo Barmalei was born on January 1st in year A and died on December 31st in year B. How many times during his lifetime was a comet visible from Earth? We believe that he could see the comet even as a baby or a very old man, i.e. if she arrived in year A or B.
The program takes as input three integers A, B and C (1 ≤ A ≤ B ≤ 2×109 , 1 ≤ C ≤ 2×109 ) and should output a single integer – number of times the comet has been
visible between years A and B inclusive.
|
Enter |
Output |
Note |
|
1850
1900
50
|
2 |
The comet flew near the Earth in 1850 and 1900. Barmaleo Barmalei caught both times. |
| |
![]()
|
|
Темы:
Formula derivation
For the opening ceremony of the Olympiad in Informatics, the organizers are looking for a suitable hall. The hall should have the shape of a rectangle, the length of each side of which is a positive integer.
In order for all participants of the ceremony to fit in the hall, and at the same time it does not look too empty, the area of \u200b\u200bthe hall should be between A and B square meters, inclusive.
In order to place posters on the walls of the hall telling about the successes of schoolchildren at the Olympiads, but at the same time not to create the feeling that there are too few successes, the perimeter of the hall should be between C and D meters, inclusive.
Before making the final choice, the organizers of the Olympiad decided to look at one hall of each suitable size. Halls with dimensions Y × Z and Z.times. Y are considered the same. In order to understand the amount of work required to view the halls, the organizers asked how many different halls satisfy the above restrictions. It is required to write a program that, given A, B, C and D, determines the number of different halls, the area of \u200b\u200bwhich is in the range from A to B, and the perimeter — from C to D, inclusive.
Input file format
The input file contains four space-separated integers: A, B, C, and D (1<=A<=B<=109 , 4<=C<=D<=109 ).
Output file format
The output file must contain a single number — desired number of halls.
Input:
2 10 4 8
Output:
3
Explanations for the example
In the example, the halls of the following sizes satisfy the constraints: 1 x times; 2.1 x 3.2 x 2
| |
![]()
|
|
Темы:
Formula derivation
In the city where friends Andrei and Boris live, the subway consists of a single ring line along which n stations numbered from 1 to n are located at equal distances from each other. The section of the metro line between two neighboring stations is called a span.
Trains on the Circle Line move both clockwise and counterclockwise, so in order to get from one station to another, a passenger can choose the direction in which they need to travel fewer hauls. The minimum number of hauls that you need to travel to get from one station to another, we call the distance between stations.
Friends noticed that the following condition is fulfilled: if you think of some station X and write out two numbers for it: Da — distance from the station where Andrey lives to station X and Db — distance from the station where Boris lives to station X, then the resulting pair of numbers [Da, Db] will uniquely define station X.
For example, if n = 4, Andrey lives at station 1, and Boris lives at station 2, then station 1 is given by the pair [0, 1], station 2 — pair [1, 0], station 3 — pair [2, 1] and station 4 — pair [1, 2].
Their classmate Sergei lives in a nearby town and does not know which stations Andrei and Boris live at. To find friends, he became interested in how many options for pairs of stations A, B exist, such that if Andrey lives at station A, and Boris — at station B, then the above condition is met.
It is required to write a program that, by the number of stations n on the ring line, determines the required number of options.
Input file format
The first line of the input file contains a single integer n (3 ≤ n ≤ 40 000).
Output file format
The output file must contain a single number — desired number of options.
Examples of input and output files
Explanations for examples
In the first example, the following options are suitable:
- Andrey lives at station 1, and Boris at station 2;
- Andrey lives at station 1, and Boris at station 4;
- Andrey lives at station 2, and Boris at station 1;
- Andrey lives at station 2, and Boris at station 3;
- Andrey lives at station 3, and Boris at station 2;
- Andrey lives at station 3, and Boris at station 4;
- Andrey lives at station 4, and Boris at station 1;
- Andrey lives at station 4, and Boris at station 3.
| |
![]()
|
|
Темы:
Formula derivation
Bolik solves a logical problem. To solve it, he first made N basic assumptions. After that, the following process occurs: Holmes breaks all the assumptions into pairs, from each pair he discards the least probable assumption (the assumptions are such that there is always the least probable). If it turned out that some assumption was not enough, then Bolik leaves it for consideration. The algorithm repeats until Bolik has the last guess left.
Bolick is also used to counting the number of inferences he has made. So, for example, if the 11th and 31st assumptions are considered and the 11th is discarded, then Bolik made one logical conclusion. If, for example, the 238th assumption lacked a pair, then Bolik leaves it for consideration, but, of course, does not consider this action as a logical conclusion. Moreover, Bolick checks the last output twice.
Now Bolik wants to understand from the existing number of basic assumptions how many logical conclusions he has to draw.
Input Format
The input is a natural number N (1 ≤ N ≤ 10218) — number of base guesses.
Output format
Print a single integer — number of inferences.
Example
| |
![]()
|
|
Темы:
Formula derivation
Lyolik decided to host the Olympiad at his school. To do this, he needs to buy a lot of paper packages. Lelik was very lucky because a large stationery store announced two promotions: "Buy A of the same items and get another item for free" and "Buy B items for the price of B-1 item".
Lyolik found out that one pack of paper in this store costs n rubles. Now he wants to determine how many packs of paper he can buy for p rubles. Help him.
Input Format
The input is four natural numbers separated by spaces: A, B, p and n (1 ≤ A ≤ 100, 2 ≤ B ≤ 100, 1 ≤ p, n 10000).
Output format
Print a single integer — the maximum number of packages of paper that Lyolik can buy.
Example
|
Enter |
Output |
|
4 4 13 2
|
8 |
|
3 4 8 3
|
2 |
|
3 4 7 1
|
9 |
Notes
In the first example, using the second share twice, you can buy 8 packs of paper, paying for 6.
In the second example, promotions cannot be used.
In the third example, you can use each of the two shares once and buy another package of paper with the remaining ruble.
| |
![]()
|
|
Темы:
Formula derivation
Denis also decided to start manufacturing and selling spinners, but he believes that a spinner can only have three or four blades. It has exactly M blades that it can attach to bases, and an unlimited supply of bases. He wants to make some 3-blade spinners and some 4-blade spinners so that all M blades are used. Decide how many spinners of each kind it should produce.
The program receives as input one positive integer M, not exceeding 2×109
, – the number of blades that Denis has.
The program should output two integers – the number of spinners with 3 blades and the number of spinners with 4 blades that Denis must produce. If the task has
several solutions, you need to display any of them. If Denis cannot use exactly M blades to produce spinners, the program should output two numbers 0.
|
Enter |
Output |
Note |
|
10 |
2
1 |
10=3.times. 2 + 4 x 1 |
|
1 |
0
0 |
It is not possible to produce spinners in such a way that
the total number of blades was 1.
|
| |
![]()
|
|
Темы:
Cycles
Formula derivation
The biscuit machine produces B biscuits at the following times: A seconds, 2A seconds, 3A seconds and every subsequent multiple of A seconds after power on. Determine how many cookies the machine will have produced by time T+0.5 seconds after power on.
Input
The program takes as input one string containing three numbers A, B and T. 1 <= A, B, T <= 20, A <= T. All numbers are positive integers.
Imprint
Print one number - the answer to the problem.
Examples
| # |
Input |
Output |
| 1 |
3 5 7 |
10 |
| 2 |
3 2 9 |
6 |
| |
![]()
|
|
Темы:
Whole numbers
Formula derivation
The values of two points of time belonging to the same day are given: hours, minutes and seconds for each of the points of time. It is known that the second moment of time came not earlier than the first. Determine how many seconds have elapsed between two points in time.
Input
The program receives three integers as input — hours, minutes, seconds representing the first point in time and three integers representing the second point in time.
Imprint
Print the number of seconds between these times.
Examples
| # |
Input |
Output |
| 1 |
1
1
1
2
2
2
|
3661
|
| 2 |
1
2
thirty
1
3
20
|
50
|
| |
![]()
|
|
Темы:
Whole numbers
Formula derivation
At the Department of "Applied Informatics" University N in the new academic year recruited three groups of first-year students. For practical exercises, it is necessary to equip a new audience with laboratory tables. No more than four students can sit at each such table, and all students must be from the same group. The audience has the opportunity to simultaneously accommodate students from three groups at once.
Determine the minimum number of tables to be purchased.
Input
The program receives as input three natural numbers (one number per line): the number of students in each of the three groups.
Imprint
Print the answer to the problem.
Examples
| # |
Input |
Output |
| 1 |
15
20
24 |
15 |
| |
![]()
|
|
Темы:
Mo algorithm
Formula derivation
There is an array of natural numbers a1, a2, ..., an. Consider some of its subarrays al, al + 1, ..., ar, where 1 ≤ l ≤ r ≤ n, and for each natural number s denote by Ks the number of occurrences of the number s in this subarray. Let's call the cardinality of a subarray the sum of the products Ks·Ks·s over all distinct integers s. Since the number of different numbers in the array is finite, the sum contains only a finite number of non-zero terms.
It is necessary to calculate the cardinalities of each of the t given subarrays.
Input
The first line contains two integers n and t (1 ≤ n, t ≤ 200000) — the length of the array and the number of requests, respectively.
The second line contains n natural numbers ai (1 ≤ ai ≤ 106) — array elements.
The next t lines contain two positive integers l and r (1 ≤ l ≤ r ≤ n) — indexes of the left and right ends of the corresponding subarray.
Imprint
Print t lines, where the i-th line contains the only natural number — cardinality of the i-th query subarray.
Examples:
| Input |
Output |
3 2
1 2 1
1 2
1 3
| 3
6 |
8 3
1 1 2 2 1 3 1 1
27
16
27 |
20
20
20 |
| |
![]()
|
|
Темы:
hash
Formula derivation
You are given t queries, in each of which you are given a string s consisting of lowercase Latin letters, a number p and a number mod.
For each query, compute a polynomial hash modulo base p of the string that is the string s, where each letter is duplicated. That is, if s = "isaac", then you need to calculate the hash from the string "iissaaaacc".
Input:
The first line contains the number t - the number of requests.
Then there are t lines, each containing space-separated s (1 <= |s| <= 20), p (1 <= p <= 105) and mod ( 1 <= mod <= 108).
Output:
Print the responses to the queries, each on a separate line.
Example:
| Input |
Output |
2
isaac 12345 87654321
newton 54321 12345678 |
8829000
9632318 |
| |
![]()
|
|
Темы:
Formula derivation
Farmer John is photographing N of his cows (2≤N≤1000).
Each cow has an integer - "Breed ID" in the range 1*100. FD split all cows into disjoint groups (in other words, put each cow in exactly one group) and then arrange the groups so that the sum of the "Breed ID" cows in the first group were even, in the second - odd, etc., alternating even and odd.
What is the maximum number of groups that a FD can form?
Input
The first line of input contains the number N. The next line contains N space-separated integers representing the "breed ID".
Imprint
The maximum possible number of groups in the PD photo. It can be proved that there will always be at least one group.
Examples
| # |
Input |
Output |
Explanations |
| 1 |
7
1 3 5 7 9 11 13
|
3 |
In this example, one way to form the maximum number (3) of groups is as follows:
1 group: 1 3
Group 2: 5 7 9
3rd group: 11 13 |
| 2 |
7
11 2 17 13 1 15 3
|
5 |
In this example, one way to form the maximum number (5) of groups is as follows: 1 group: 2
Group 2: 11
3rd group: 13 1
4th group: 15
5th group: 17 3. |
| |
![]()
|
|
Темы:
Formula derivation
Farmer John has N cows (1 ≤ N ≤ 20) with heights a1…aN. His barn has N stalls with maximum heights b1…bN (so for example b5=17 means no cows with a height more than 17 can be placed in a stall 5). In how many different ways can the FD place the cows into the stalls so that the height constraint is met for each stall.
Input
The first line contains N. The second line contains N numbers a1, a2,…,aN separated by single spaces. The third line contains N numbers b1,b2,…,bN separated by single spaces. All values are integers in the interval [1,109].
Imprint
The number of ways the FD can place cows in the stalls so that the height limit is satisfied for each stall. Note that the answer can be very large, so it requires a 64-bit integer variable such as "long long" in C++.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
4
1 2 3 4
2 4 3 4
|
8 |
In this example, we cannot place the third cow in the first stall because 3=a3>b1=2. Likewise, we cannot place the 4th cow in the 1st or 3rd stall. One of 8 placement options: Cow 1 to Stall 1, Cow 2 to Stall 2, Cow 3 to Stall 3, Cow 4 to Stall 4. |
| |
![]()
|
|
Темы:
Strings
Conditional operator
Formula derivation
Gromozeka respects chessboard games. Gromozeka has a hungry pawn on a regular 8x8 board. A hungry pawn eats some opponent’s piece every move (i.e. it can move diagonally forward 1 square to the right or left, it cannot move back). Gromozeka, without looking at the board, learned to determine whether a hungry pawn can move from one square of the board to another. It is impossible to turn into a queen to a hungry pawn.
Write a program with which you could also easily check Gromozeka.
Input
The program receives as input two cells of the chessboard in chess notation. First, the cell where the hungry pawn stands, and then, after a gap, the cell where the hungry pawn must go.
Imprint
Print the word YES (in capital letters) if a hungry pawn can move from the first cell to the second, and NO otherwise.
The board has a size of 8x8, the verticals are numbered in small Latin letters from a to h, the horizontals are numbered from 1 to 8. The starting and ending cells do not match.
Examples
| # |
Input |
Output |
| 1 |
a1 b2 |
YES |
| 2 |
b2 a1 |
NO |
| 3 |
a1 h7 |
NO |
| |
![]()
|
|
Темы:
Formula derivation
Bust
Farmer John wants to create a triangular pasture for his cows.
There are N fence posts in total (3 ≤ N ≤ 100) as distinct (X1,Y1)…(XN, YN) points on the farm map. He can choose three of them to form the vertices of a triangular pasture, but so that one of the sides is parallel to the x-axis and the other is parallel to the y-axis.
What is the sum of the areas of all possible pastures that a FD can form?
Input
The first line contains N.
Each of the following N lines contains two integers Xi and Yi, each in the interval −104…104 inclusive, describing the position of the post.
Imprint
Since the sum of areas may not be an integer and very large, print the remainder after dividing twice the sum of areas by 109+7.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
4
0 0
0 1
10
1 2
|
3 |
Points (0,0), (1,0), (1,2) form a triangle with area 1.
Points (0,0), (1,0), (0,1) form a triangle with area 0.5.
So the answer is 2⋅(1+0.5)=3. |
| |
![]()
|
|
Темы:
Formula derivation
Implementation task
Simulation tasks
The N cows (1 ≤ N ≤ 100) of Farmer John are lined up. The i-th cow on the left has label i, for all 1≤i≤N.
The FD ordered the cows to repeat exactly K (1 ≤ K ≤109) times the following two-step process:
The sequence of cows at positions A1…A2 on the left reverses their order (1≤A1<A2≤N).
Then the sequence of cows at positions B1…B2 on the left reverses their order (1≤B1<B2≤N).
Output the resulting order of cows for all i 1 ≤ i≤ N after running this process exactly K times.
Input
The first line contains N and K. The second line contains A1 and A2, the third line contains B1 and B2.
Imprint
On the i-th line print the label of the i-th cow on the left after the process of all exchanges is completed.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
7 2
25
3 7
|
1
2
4
3
5
7
6
|
Initially, the order of cows from left to right is [1,2,3,4,5,6,7]
After the first step of the process, the order will be [1,5,4,3,2,6,7]
After the second step of the process, the order will become [1,5,7,6,2,3,4].
Repeating both steps one more time we get the result shown in the output. |
| |
![]()
|
|
Темы:
Formula derivation
Bust
Farmer John has N spotted cows and N spotless cows. As a geneticist, FD is certain that the spots on his cows are caused by a mutation in the cow's genome.
For a lot of money, the FD issued the genomes of his cows. Each genome is a string of length M, consisting of four characters A, C, G, T. When he wrote out the genomes of all cows, he got the table below for N=3:
Position: 1 2 3 4 5 6 7 ... M
Spotted Cow 1: A A T C C C A ... T
Spotted Cow 2: G A T T G C A ... A
Spotted Cow 3: G G T C G C A ... A
Cow without spots 1: A C T C C C A ... G
Cow without spots 2: A G T T G C A ... T
Cow without spots 3: A G T T C C A ... T
Looking closely at this table, he suggested that positions 2 and 4 might be responsible for the spotting. Because by looking at the characters in these positions, the FD can predict which of his cows are spotted and which are not (for example, if he sees G and C, then the cow is not spotted).
FD suggested that it could be explained by a set of three different positions. Help him count the number of three different positions that could explain the spotting.
INPUT FORMAT:
The first input line contains NN (1≤N≤500) and MM (3≤M≤50). Each of the following N lines contains M characters. This is a description of the genomes of spotted cows. The next N lines describe the genomes of spotless cows.
OUTPUT FORMAT:
Compute the number of sets from three different positions that can explain the spotting. A plurality of three different positions can explain spotting if spotting can be predicted absolutely accurately for a population of FD cows by analyzing these three positions of the genome.
| Input |
Output |
|
3 8
ATCCCAT
GATTGCAA
GGTCGCAA
ACTCCAG
ACTCGCAT
ACTTCCAT
|
22 |
| |
![]()
|
|
Темы:
Formula derivation
Fast exponentiation
Permutations
N cows (1 ≤ N ≤ 105) Farmer John stand in a row. The i-th cow on the left has label i (1 ≤ i ≤ N).
FD gave the cows M pairs of integers s (L1,R1)…(LM,RM), where 1 ≤ M≤ 100. Then he told the cows to repeat exactly K (1 ≤ K ≤ 109) times the process of M steps:
For every i from 1 to M:
The sequence of cows in positions Li…Ri on the left reverses their order.
Print the labels of all cows from left to right for each i, (1 ≤ i ≤ N) after the process is completed.
Input
The first line contains the numbers N, M, K. For each 1 ≤ i≤ M string i+1 contains Li and Ri, two integers in the interval 1…N, where Li<Ri.
Imprint
On the i-th line of the output, print the i-th element of the array after executing all instructions K times.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
7 2 2
25
3 7
|
1
2
4
3
5
7
6
|
Initially, the order of cows from left to right is [1,2,3,4,5,6,7]
After the first step of the process, the order will be [1,5,4,3,2,6,7]
After the second step of the process, the order will become [1,5,7,6,2,3,4].
Repeating both steps one more time we get the result shown in the output. |
| |
![]()
|
|
Темы:
Sorting algorithms
Formula derivation
Farmer John wants to create a triangular pasture for his cows.
There are N fence posts (3 ≤ N ≤ 105) as different (X1,Y1)…(X< sub>N,YN) points on the farm map. He can choose three of them to form the vertices of a triangular pasture, but so that one of the sides is parallel to the x-axis and the other is parallel to the y-axis.
What is the sum of the areas of all possible pastures that a FD can form?
Input
The first line contains N.
Each of the following N lines contains two integers Xi and Yi, each in the interval −104…104 inclusive, describing the position of the post.
Imprint
Since the sum of areas may not be an integer and very large, print the remainder after dividing twice the sum of areas by 109+7.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
4
0 0
0 1
10
1 2
|
3 |
Points (0,0), (1,0), (1,2) form a triangle with area 1.
Points (0,0), (1,0), (0,1) form a triangle with area 0.5.
So the answer is 2⋅(1+0.5)=3. |
| |
![]()
|
|
Темы:
Depth walk
Formula derivation
Farmer John's new barn consists of N rooms (2 ≤ N ≤ 2500), consecutively numbered 1 x hellip; N, and N x minus; 1 corridors. Each corridor connects a pair of rooms in such a way that it is possible to go from one room to any through a series of corridors.
Each room in the barn has a round clock on the wall with the standard 1…12 on the front. However, this clock has only one hand, which always points exactly to one of the integers (it never points between two of those numbers).
Cow Besi wants to synchronize all the clocks in the barn so that they all point to the number 12. But with her cow thinking, every time she enters the room, she moves the hand forward one position. For example, if the arrow was pointing at 5, Besie will move the hand to 6. If the clock was pointing to 12, she will move the hand to 1. If Besie enters the room multiple times, she will move the hand each time she enters.
Determine the numbers of rooms in which Besie can start the journey through the barn to set all arrows to 12. Note that Besie does not move the arrow in the starting room at the beginning of the path and moves each time she enters it. The arrows themselves do not move. Besi entering the corridor must reach the end and enter the room at the end of the corridor. She can't turn back inside the hallway to re-enter the room she left.
Input
The first line of input contains N. The next line contains N integers, each in the range 1*12, indicating the initial positions of the arrows in each room. Each of the following N−1 lines describes a corridor with two integers a and b, each in the range 1…N, and the numbers of the rooms connected by this corridor.
Imprint
Print the numbers of the rooms Besi can start in to set all clocks to 12.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
4
11 10 11 11
12
2 3
24
|
1 |
In this example, Besi can only set all arrows to 12 if she starts in room 2 (e.g. moving like this: 1, 2, 3, 2, 4. |
| |
![]()
|
|
Темы:
Formula derivation
The checkered field consists of white cells. The field size is H rows and W columns. You need to select h rows and w columns and fill in all the cells contained in those rows or columns. How many white cells will remain after painting?
Input
The first line contains 2 numbers: H and W (1 <= H, W <= 20). The second line contains 2 numbers: h and w (1 <= h <= H, 1 <= w <= W).
Imprint
Print the answer to the problem.
Examples
| # |
Input |
Output |
| 1 |
3 2
2 1
| 1 |
| 2 |
5 5
2 3
| 6 |
| 3 |
2 4
24 |
0 |
| |
![]()
|
|
Темы:
Formula derivation
Dunno and his friend Gunka are playing a game. The game consists of N moves. On each turn, each player plays one of the two gestures, Rock and Paper, as in Rock-Paper-Scissors, under the following conditions:
- After each move
(number of times the player played Paper) <= (number of times the player played Rock).
- The score of each player is calculated by the formula:
(number of turns the player wins) - (number of turns the player loses),
where the result of each move is determined by the rules of "rock-paper-scissors".
For those unfamiliar with the Rock-Paper-Tailing game, if one player plays Rock and the other plays Paper, the last player wins and the first player loses. If both players play with the same gesture, the round is considered a draw and neither player wins or loses.
Using a magic wand Dunno was able to foresee the gesture that Gunka would use in each of the N moves before the start of the game. Plan out Dunno's gestures at every turn to maximize his score.
The gesture that Gunka will play on each move is specified by the s string. If i-th (1 <= i <= N) character in s is equal to g, then Gunka will play "Stone" on ith move. Similarly, if the i-th (1 <= i <= N) character s in p, Gunka will play Paper on < code>i-th move.
Input
The input is one string s of length N. Each character in the string s is g or p >. The gestures represented by s satisfy the game condition.
Imprint
Print the maximum possible score of Dunno.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
gpg |
0 |
Performing the same gesture with an opponent in each step is worth 0 points, which is the maximum possible result. |
| 2 |
ggppgggpgg |
2 |
For example, consider playing gestures in the following order: Rock, Paper, Rock, Paper, Rock, Rock, Paper, Paper, Rock, Paper. This strategy yields three wins and one loss, resulting in 2, which is the highest possible score. |
| |
![]()
|
|
Темы:
Formula derivation
Vintik and Shpuntin tested new cars. The distance around the Flower City was covered by Vintik's car in t1 seconds, the speedometer showed the speed of V m/s all the way. Shpuntik's car covered the same distance around the Flower City in t2 seconds, while Shpuntik's speedometer was broken. Help Shpuntik determine how fast (in m/s) he was driving.
Input
Input 3 integers: t1(1<=t1<=100), V< /code>(1<=V<=100) and t2 (1<=t2 <=100).
Imprint
Print one number - the answer to the problem.
Example
| # |
Input |
Output |
| 1 |
10 12 15 |
8.0 |
| |
![]()
|
|
Темы:
Formula derivation
Dunno was trained by Toropyzhka to walk faster. Before training, he walked a path of S meters in t1 seconds. After training Dunno's speed increased by P%. Write a program that determines which path (in meters) Dunno will walk in t2 seconds after training with Toropyzhka.
Input
Four integers as input: S (1<=S<=100), t1(1<=t 1<=100), P (1<=P<=100) and t 2 (1<=t2<=100).
Imprint
Print one number - the answer to the problem.
Example
| # |
Input |
Output |
| 1 |
20 5 40 10 |
56.0 |
| |
![]()
|
|
Темы:
Formula derivation
There is a sequence of length N: A1, A2, ..., AN. Initially, this sequence is a permutation of 1, 2, ..., N. In this sequence, Alice can perform the following operation:
1) select K consecutive elements in sequence;
2) then replace the value of each selected element with the minimum value among the selected elements.
Alice wants to equalize all the elements in this sequence by repeating the above operation a number of times.
Find the minimum number of necessary operations.
It can be proved that, under the constraints of this problem, this goal is always achievable.
Input
The first line specifies two integers N and K (2<=K<=N<=100000). The second line specifies a sequence of integers A1, A2, ..., AN - permutation of numbers from 1 to N (each number in the sequence is different, 1<=Ai <=N).
Imprint
Print the minimum number of required operations.
Examples
| # |
Input |
Output |
| 1 |
4 3
2 3 1 4
| 2 |
| 2 |
3 3
1 2 3
| 1 |
| 3 |
8 3
7 3 1 8 4 6 2 5
| 4 |
| |
![]()
|
|
Темы:
Whole numbers
Formula derivation
Gromozeka loves programming competitions. Today he will take part in the competition in STCoder. This site uses a 24-hour clock. For example, 21:00. referred to as «21 o'clock».
The current time is A hours and the competition will start exactly in B hours. Determine the start time of the competition? Give your answer in 24-hour format.
Input
The input string contains two integers A and B (\(0<=A,B<=23\)) separated by one space.
Imprint
Print the contest start hour in 24-hour format.
Examples
| # |
Input |
Output |
| 1 |
9 12 |
21 |
| 2 |
19 0 |
19 |
| 3 |
23 2 |
1 |
| |
![]()
|
|
Темы:
Formula derivation
Whole numbers
The turtle crawls on the floor, which is laid with square tiles with side A see. The start of the Turtle's path is at X. The turtle managed to crawl a distance of D cm before the owner picked it up. Determine how many cells (partially or whole) the Turtle managed to crawl through.
Input
The first line contains the number A – side length of one tile. The second line contains the number X - the coordinate of the point from which the Turtle started its journey. The third line - the number D - the distance that the Turtle crawled. The OX axis is directed to the right. The last tile in the row on which the Turtle is crawling is at the origin. All numbers are integers not exceeding \(2\cdot10^9 \), numbers A, D – positive, number X – positive or equal to 0.
Imprint
Output one number – the number of tiles that the Turtle has fully or partially crawled through.
It is considered that the Turtle has crawled through the tile if the conditionally drawn line of the Turtle's path has a non-zero length, that is, the touch of the path line and the edge of the tile is not considered.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
10
15
35 |
4 |
Tile side (cell side in the picture) A = 10.
The turtle started at X = 15 and passed 35.
The turtle has completely or partially passed 4 tiles.
 |
| |
![]()
|
|
Темы:
Formula derivation
You are given non-negative integers a and b (a<=b) and a positive integer x. How many integers from a to b inclusive are divisible by x?
Input
One line contains three numbers a, b and x (\(0<=a<=b<=10^{18}\), \(1<=x<=10^{18}\)).
Imprint
Display the answer to the problem.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
4 8 2 |
3 |
There are three integers from 4 to 8 inclusive that are divisible by 2: 4, 6 and 8. |
| 2 |
0 5 1 |
6 |
There are six integers from 0 to 5 inclusive that are divisible by 1: 0, 1, 2, 3, 4 and 5. |
| 3 |
9 9 2 |
0 |
There is no integer between 9 and 9 inclusive that is divisible by 2. |
| 4 |
1 1000000000000000000 3 |
333333333333333333 |
Beware of integer overflows! |
| |
![]()
|
|
Темы:
Formula derivation
The pen cost K rubles. On September 1, the cost of a pen increased by exactly P percent. Determine how many pens you can buy for S rubles after the rise in price.
The program receives three positive integers as input. The first number is K – the cost of the pen in rubles before the rise in price. Second number P – pen price increase
in percentages. Third number S – available amount of money. The numbers K and S do not exceed 107 , the number P does not exceed 100.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
33
5
100
| 2 |
The pen cost 33 rubles. After a 5% rise in price, the pen will cost 34 rubles 65 kopecks (note that, since the initial
the price of the pen was an integer number of rubles, after the rise in price, the cost of the pen will be expressed in an integer number of rubles and kopecks).
For 100 rubles after the rise in price, you can buy 2 pens. |
| |
![]()
|
|
Темы:
Formula derivation
Masha loves even numbers, and Misha – odd. Therefore, they are always happy if they meet numbers they like.
Today they met all integers from A to B inclusive. Masha decided to calculate the sum of all even numbers from A to B, and Misha – the sum of all the odd ones, after which they began to argue who got the sum more. Help them – find the difference
between Masha's sum and Misha's sum.
The program receives as input two positive integers A and B, not exceeding 2×109.
The program should output a single number – the difference between the sum of even numbers and the sum of odd numbers from A to B.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
3
6 |
2 |
The sum of even numbers is 4 + 6 = 10, the sum of odd numbers
is 3 + 5 = 8, the difference is 2. |
| 2 |
3
7 |
-5 |
The sum of even numbers is 4 + 6 = 10, the sum of odd numbers
is 3 + 5 + 7 = 15, the difference is −5. |
| |
![]()
|