| Problem description | | Progress |
|
Темы:
Real numbers
Formula derivation
Write a program that calculates the y value.
\(y = \frac a {b \cdot c}\)
Input
The input is 3 integers a, b, c (b, c > 0).
Imprint
Output the value y.
Example
| # |
Input |
Output |
| 1 |
4 2 3 |
0.67 |
| 2 |
1 2 1 |
0.5 |
| |
![]()
|
|
Темы:
Formula derivation
Real numbers
Write a program that calculates the value of y.
\(y = 5.45 \cdot \frac {a + 2 \cdot b} {2-a}\)
Input
The input is 2 integers a (a>2) and b.
Imprint
Print the value y.
Examples
| # |
Input |
Output |
| 1 |
4 2 |
-21.80 |
| 2 |
1 2 |
27.25 |
| |
![]()
|
|
Темы:
Real numbers
Formula derivation
Write a program that calculates the value of y.
\(y = \frac {a + b} {2}\)
Input
The input is 2 integers a and b.
Imprint
Print the value y.
Examples
| # |
Input |
Output |
| 1 |
2 2 |
2 |
| 2 |
1 2 |
1.5 |
| |
![]()
|
|
Темы:
Real numbers
Formula derivation
Write a program that calculates the value of y.
\(y = \frac {-1} {x^2}\)
Input
The input is an integer x (x > 0).
Imprint
Print the value y.
Examples
| # |
Input |
Output |
| 1 |
2 |
-0.25 |
| 2 |
1 |
-1 |
| |
![]()
|
|
Темы:
Real numbers
Input format
Given a positive real number X.
Output format
Output its fractional part.
Example
| |
![]()
|
|
Темы:
Real numbers
Conditional operator
The holidays began, and Maxim came to visit his grandparents, but not at all to the village, as you probably thought. Maxim's grandparents live in a very cultured city with legendary bad weather — it often rains here.
And now, as soon as Maxim left the station building, a downpour began. The umbrella, according to all the laws of meanness, lies at the bottom of his suitcase, and he does not want to climb after it at all. Yes, and here — There is a bus stop very close, under which you can hide from the rain. You just need to cross the street, and that's it! "It's not all that simple," — came to Maxim's mind. And indeed — does not happen.
The fact is that on the street that separates Maxim from the stop, the asphalt is being changed. The old layer of asphalt has already been removed (there are now pits, so it’s impossible to pass there), and now an asphalt paver is courageously crawling along the street, approaching Maxim, at a speed of v2 m / min, leaving behind a new, neatly laid asphalt. True, before the new asphalt can be walked on, it must cool down for T minutes. The paver has just started work, so all the asphalt behind it was poured yesterday and has already cooled down.
Of course, Maxim does not want to get wet, so he tries to get to the other side of the street as quickly as possible. He runs at a speed of v1 m/min. He also knows the width of the street — L m. Maxim can walk along the street along the sidewalk as much as he wants. He wants to be on the road as little as possible, so he only crosses the street perpendicularly.
Input
Given integers L, D, T, v1, v2 — street width, distance to the paver, time that the asphalt cools down (in minutes), Maxim's speed and the speed of the paver. (1 ≤ L ≤ 100, 1 ≤ D ≤ 100, 1 ≤ T ≤ 100, 1&thinsp ;≤ v1 ≤ 100, 1 ≤ v2 ≤ 100).
Imprint
Print one number — the time in minutes it takes Maxim to get to the other side of the street.
Examples
| # |
Input |
Output |
| 1 |
4 9 3 2 1 |
6.0 |
| 2 |
1 1 1 3 1 |
0.666666666667 |
| |
![]()
|
|
Темы:
Greedy Algorithm
Real numbers
Given a valid equality of the form a1+a2+…+aN=b1+b2+…bM, where a1,a2,…,aN, b1,b2,…,bM – some real (not necessarily integer) numbers. Required to "round up" this is equality, i.e. get a new correct equality c1+c2+…+cN=d1+d2+…+dM, where c1,c2,…,cN< /sub>,d1,d2,…,dM — integers, and at the same time c1 is obtained by rounding the number a1 up or down to an integer (for example, the number 1.7 can be rounded up to either 1 or 2) , c2 obtained by rounding a2, …, cN – rounding aN, d1 – rounding b1, …, dM – rounding bM. If any of the numbers in the original equality was an integer, it should remain unchanged.
Input
The input file is given first the number N, then N numbers a1, a2, …, aN, then the number M, then the numbers b1, b2, …, bM. Each number is given on a separate line. M and N – natural numbers not exceeding 1000. Other numbers — real, each of them does not exceed 1000 in absolute value and contains no more than 6 digits after the decimal point. Here a1+a2+…+aN=b1+b2 +…bM.
Imprint
If "round up" equality is possible, then output the numbers c1,c2,…,cN, and then the numbers d 1,d2,…,dM. All numbers must be integers and printed without a decimal point. Numbers must be separated by spaces or newlines. If there are several solutions, print any of them.
If it is impossible to round the original equality to a true integer equality, print a single number 0.
Examples
| # |
Input |
Output |
Explanation |
| 1 |
3
0.15
-3.000
2.7
1
-0.15
| 1
-3
2
0 |
Note that –3 can only be rounded to –3, while 0.15 can be rounded to either 0 or 1, 2.7 – up to 2 or up to 3, –0.15 – up to –1 or up to 0. The given solution is not the only one: the following rounding is also correct, for example: 1+(–3)+2=0
|
| 2 |
2
1.7
2.5
3
1
2.000
1.20 |
2
2
1
2
1 |
The given solution 1+3=1+2+1 is not the only one. The correct answers are also 2+2=1+2+1 and 2+3=1+2+2.
|
| 3 |
1
0.5
1
0.5
| 0
0 |
Here, both 1=1 and 0=0 are correct. |
| |
![]()
|
|
Темы:
Cycles
Real numbers
The nutrition of a schoolchild, with proper organization, should provide the content of proteins, fats and carbohydrates in a ratio of 10%: 30%: 60% (an error of +/- 1% is allowed). The children's camp is compiling a menu consisting of N different products. For each product, the energy value in proteins (P), fats (F) and carbohydrates (C), as well as the amount of each type of product in menu(K).
Determine if the menu is balanced or not.
Input
The program receives several lines as input. The first line contains a natural number N (N <= 100) the number of different products. Each of the following N lines contains 4 numbers: Pi, Fi, Ci and Ki. All numbers are real, do not exceed 103.
Imprint
Print YES if the menu is balanced, and NO otherwise.
Examples
| # |
Input |
Output |
| 1 |
3
0 1 1 2
1 2 7 1
3 7 13 1
| YES |
| |
![]()
|
|
Темы:
Real numbers
Given the lengths of the two legs in a right triangle and output its area.
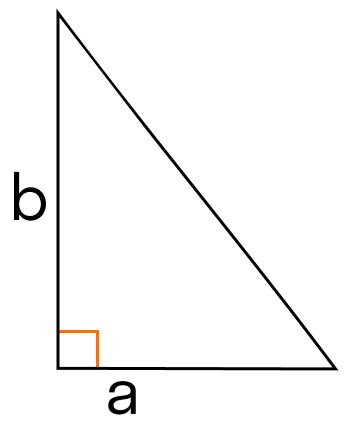
The area of a right triangle formula is \(S = {1 \over 2} \cdot a \cdot b\),
a, b - length of legs.
Input format
Given two real numbers – length of legs (a, b), each on a separate line (1 <= a, b <= 104).
Output format
Output one number - the area of a right triangle with an accuracy of at least three decimal places.
Examples
| N |
Input |
Output |
| 1 |
2.0
3.0 |
3.000 |
| 2 |
26.0
78.0 |
1014.000 |
| 3 |
3.5
7.8 |
13.650 |
| |
![]()
|
|
Темы:
Real numbers
Neznaika and Gunka decided to meet to go visit Knopochka. They ran out of their houses at the same time to meet each other. Neznaika ran with speed V1 meters per second, and Gunka with speed V2 meters per second. In how many seconds they will meet if the distance between their houses is S meters.
Input format
Given are three real numbers S, V1, V2, каждое на отдельной строке.
Output format
Outpur the answer to the problem with an accuracy of at least 6 decimal places.
Example
| N |
Input |
Output |
| 1 |
100.0
15.0
20.0 |
2.857142857142857 |
| |
![]()
|
|
Темы:
Data types
Real numbers
Write a program that calculates the square root of a number entered from the keyboard, accurate to three decimal places.
The input is a real number.
Example
Input
25.
Output
5.000
| |
![]()
|
|
Темы:
Real numbers
Write a program that calculates the length of a circle through the area of the circle.
.JPG)
The circle length from the known area of the circle can be calculated by the formula :
\(L=\sqrt{S4\pi}\) ,
\(\pi\) - number of pi;
\(S\) - area of the circle.
You can use built-in constants to get the exact value of pi.
In C++ you must write the following line at the beginning of your program
#define _USE_MATH_DEFINES
In Python, you can use a constant from the math library math.pi
Input format
Given an one real number - area of the circle S (1 <= S <= 103).
Output format
Output the circle length.
Example
| N |
Input |
Output |
| 1 |
5.0 |
7.926654595212022 |
| |
![]()
|