Module: Floyd-Algorithmus


Problem

1/10

Floyd: Anfang (C++)

Theory Click to read/hide

Dun ist eine fokussierte oder unorientierte gewichtete Zählung mit n Tops.
Der Algorithmus ermöglicht einen Abstand von jedem Top und arbeitet mit negativen Rippen.
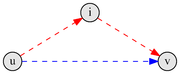
Algorithm rückt nacheinander alle I um, durch die ein kürzerer Weg zu V als jetzt verfügbar ist.

Aktuelle (sine) Route und möglicherweise kürzer (rot).

Durchführung
Bei der Eingabe des Programms handelt es sich um eine Box in Form einer Matrix von Nebenität, einer zweidimensionalen d[][] n x n, in der jedes Element die Rippenlänge zwischen den jeweiligen Spitzen einstellt.
Wenn zwischen den beiden Spitzen keine Rippe vorhanden ist, gibt es in der Matrix der Verbindungen (z.B. INT_MAX in "limits.h) eine große Anzahl, dass sie länger als die Länge einer beliebigen Reise in dieser Box sein würde); dann wäre diese Rippe immer unangebracht zu nehmen, und der Algorithmus würde richtig funktionieren.
Aber mit zwei endlosen Enden, kann es ein Nachfüllen Int und wir werden einen negativen Einfluss auf den Ausgang haben, so wäre es gut, durch eine zusätzliche Überprüfung unterstützt werden: 
wenn (seufzt)dgl.(schreit)I!(schreit)k.! INT_MAX " d(schreit)k.!(schreit)J! INT_MAX)
Am Ende wird der Algorithmus gesehen:
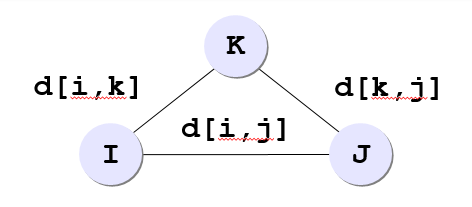
für (seufzt)in =0); kón; ++k)für (seufzt)in =0); i copy; ++i)für (seufzt)in j)0); j Besuch; ++j)wenn (seufzt)dgl.(schreit)I!(schreit)k.! INT_MAX " d(schreit)k.!(schreit)J! INT_MAX)wenn(d[i][k]+d[k][j] À d[i][j]
dgl.(schreit)I!(schreit)J! = d(schreit)I!(schreit)k.! + d(schreit)k.!(schreit)J!;


Beispielsweise ist die Anzahl:



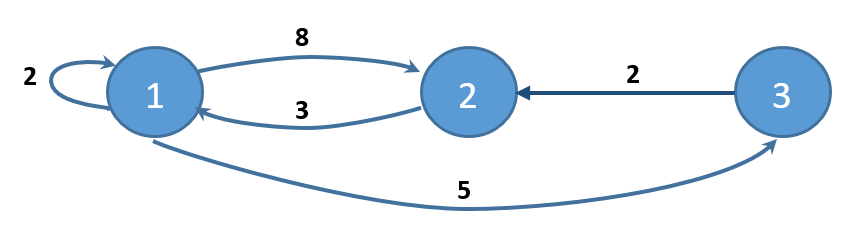
Die Anfangsgewichtsmatrix wird dann sein:
Spitzenzahl123
10)8)5.
230)INT_MAX
3INT_MAX20)

Nach der 1. Teration:
Spitzenzahl123
10)8)5.
230)8)
3INT_MAX20)

Nach 2. Teration:
Spitzenzahl123
10)8)5.
230)8)
35.20)


Nach der 3. Iteration:
Spitzenzahl123
10)75.
230)8)
35.20)



Problem

Es ist ein orientierter Graph gegeben, dessen Kanten einige nicht negative Gewichte (Längen) zugeordnet sind. Finden Sie die Länge des kürzesten Weges vom Scheitelpunkt s zum Scheitelpunkt t.
 
Eingabe
Die erste Zeile enthält drei Zahlen: die Anzahl der Eckpunkte im Diagramm N ≤50, die Eckpunktnummern s und t. Als nächstes kommt die Adjazenzmatrix des Graphen, dh N Zeilen, in denen jeweils N Zahlen geschrieben sind. die j-ten Zahl in der i-ten Zeile der Adjazenzmatrix gibt die Länge der Kante an, die vom i-ten Scheitelpunkt zum j-ten führt. Die Längen können einen beliebigen Wert zwischen 0 und 1000000 annehmen, die Zahl -1 bedeutet, dass keine entsprechende Kante vorhanden ist. Es ist garantiert, dass Nullen auf der Hauptdiagonale der Matrix stehen.
 
Ausgabe
Geben Sie eine einzelne Zahl aus, – die minimale Pfadlänge. Wenn der Pfad nicht existiert, geben Sie -1 aus.

Beispiele
№ Eingabe Ausgabe
1
3 1 2
0 -1 3
7 0 1
2 215 0
 218

time 1000 ms
memory 32 Mb
Rules for program design and list of errors in automatic problem checking

Teacher commentary

Insert the missing code snippets
C++
Write the program below 
#include <vector>
#include <iostream>
#include <climits>
using namespace std;

const int inf = INT_MAX;

int main()
{
	int n, s, t;
	cin >> n >> s >> t;
	vector<vector<int> > d(n + 1, vector<int>(n + 1,inf));
	for (int i = 0; i < n; ++i)
	{
		for (int j = 0; j < n; ++j)
		{
			int a;
			cin >> a;
			if (a != -1)
			{
				d[i + 1][j + 1] = a;
			}
		}
	}
	for (int k = 1; k <= n; ++k)
	{
		for (int i = 1; i <= n; ++i)
		{
			for (int j = 1; j <= n; ++j)
			{      
			}
		}
	}
	if (d[s][t] == inf)
	{
		cout << -1;
		return 0;
	}
	cout << d[s][t] << endl;

}

     

Program check result

To check the solution of the problem, you need to register or log in!