Schnittholz
Schnittholz (R)- es ist eine Datenstruktur, die Effizienz (d.h. Asymptotik) ermöglicht O (log n)d) Durchführung der folgenden Betriebsarten:
- die Summe/Mindestwert der Elemente der Masse im angegebenen Schnitt (a[l...r]wenn l und r zum Eingang des Algorithmus,
- Änderung der Elemente der Masse: sowohl die Änderung des Wertes eines Elements als auch die Änderung der Elemente im gesamten Teilabschnitt der Masse (d.h. es ist erlaubt, allen Elementen zuzuordnen a[l...r] jeder Wert oder addiert zu allen Elementen der Masse a[l...r] Anzahl).
Sie können entweder auf Schnitte oder Halbinteressierten pinkeln, was bedeutet, dass es ein Top gibt, das eine Funktion auf dem Schnitt hat.
[l;r]wenn Sie in Schnitte oder Halbinteressieren schreiben.
[l;r)wenn ich schreibe
halb interessiert. Es gibt keinen großen Unterschied, es wird eine halbinteressante Erklärung geben.
Schauen wir uns den DA über die Summe der Schnitte und Ergänzungen an.
Lassen Sie uns den ursprünglichen Größenbereich brechen.
n zwei etwa gleiche Geschlechter:
[0;n/2) und
[n/2;n)♪ Auf der gleichen Seite haben wir Halbdaten. Also bis wir an Größe 1. Gleichzeitig betrachten wir die Funktion aller dieser Stockwerke, deren Größe
n♪
n/2♪
n/4 usw. Es sieht aus wie ein Baum für ein Set.
{1, -5, 6, 10}♪ Am Gipfel des Gipfels sind die Grenzen seiner Unterstützung an der Spitze der Summe angegeben.
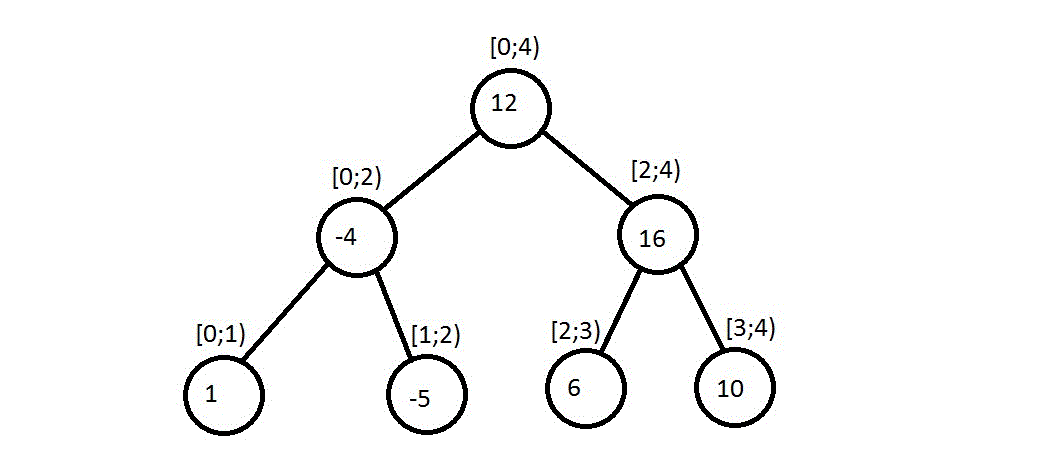
Die Figur zeigt, dass die Funktion im aktuellen Top von Kindern neu berechnet werden muss. Beispielsweise ist der Betrag im aktuellen Top die Summe im linken Kind + die Summe im rechten Kind. Das Minimum im aktuellen Top ist mindestens ein Minimum von Kindern, etc.
Es gibt auch eine leichte Unannehmlichkeit, wenn die Größe der Masse nicht ein Doppel ist, dann wird der Baum nicht so "ideal" sein. Aber in der Praxis macht es keine Unannehmlichkeiten.
Wir wenden uns nun an den Code und die Implementierung eines solchen Baumes.
Machen wir eine Struktur.
Nodewo wir die Grenzen seiner Unterstützung, die Funktion der Unterstützung (z.B. die Höhe), die Hinweise auf ihre Kinder (so bald wie möglich) und das Feld halten
addin dem wir so viel wie nötig halten, um allen Elementen der Unterstützung hinzuzufügen (was später erklärt wird, warum dies notwendig ist). Der Code sieht so aus. Wenn Sie das Feld nicht kennen, ist es eine Variable in der Struktur.
struct Node {~}
Node* links;
Node* rechts;
int lb, rb, sum, add;
?Feld
Node* left; und
Node* right; Dies sind die Marker auf der linken und rechten Söhne. Feld
int lb♪
int rb die Grenzen des Gipfels,
sum - Betrag für Unter-Assistenz
[lb;rb)Feld
add Etwas später.
Aber es gibt eine Frage: Was mit Holzblättern zu tun, haben sie keine Söhne? Infolgedessen wird es notwendig sein, die Funktion nicht durch Kinder zu überprüfen und neu zu berechnen, sondern einfach das Element der Masse (als die Grenzen des Blattes) zu vernichten.
[i;i+1)) Lassen Sie uns stattdessen ein vibrierendes Top schaffen, wo es ein neutrales Element im Ergebnisbereich (für eine Summe von 0, für die Produktion 1, für minimale Unendlichkeit) geben wird.
Code
Node* Leere = neue Node({NULL, NULL, 0, 0, 0 });Wer weiß es nicht,
{} bedeutet der Designer, d.h. die Richtung des Index auf die Struktur des Feldes
left und
right gleich
NULLFelder
lb♪
rb♪
sum♪
add gleich
0♪
NULL - ein Indikator für nichts.
Wenn das Top etabliert ist, bauen wir einen Baum. Schreibe die Funktion
builddie die Baumstruktur selbst bauen wird, bis die Funktion gezählt ist.
Wir werden dies wie folgt tun: Wir werden den aktuellen Gipfel an die Funktion der Grenze übergeben können. Wenn unser aktuelles Blattoberteil, gehen wir zurück auf die neue Spitze, wo unsere aktuellen Grenzen sind, die Höhe von 0, das Feld.
add Wir brauchen noch nichts hinzuzufügen, und Kinder sind fiktive Tops, das ist.
Empty♪ Wenn das aktuelle Top kein Blatt ist, dann starten wir unsere Funktion.
build(l, mid) und
build(mid, r)wenn
mid = (l + r) / 2♪ Also bauen wir die Söhne der aktuellen Spitze. Sobald wir gebaut wurden, haben wir das linke Kind zurück.
build(l, mid)das richtige Kind aufgrund der Umsetzung
build(mid, r)Felder
lb und
rb unsere aktuellen Spitzen, die Felder.
sum und
add 0.
Code
Node* build(int l, int r) {~}
wenn (l + 1 == sync, korrigiert von elderman == @elder_man
neue Node zurückgeben ({Empty, Leer, l, r, 0, 0});
♪
int mid = (l + r) / 2;
Node* nleft = build(l, mid); / Bau des linken Sohnes
Node* nright = build(mid, r); / rechter Sohn Gebäude
neue Node({nleft, nright, l, r, 0, 0 } zurückgeben;
♪Es wird wie ein Baum in Größe aussehen L 347 vom 20.12.2013, S. 1). Also starten wir eine Funktion.
build(0, 4)♪
Jetzt betrachten wir die asymptotische Funktion.
build Größe Reichweite
n♪
Wie zuvor beschrieben, werden wir zwei annähernd gleiche Teile teilen, nehmen diese Teile mehr und so weiter, bis wir die Größe 1 erreichen. Wie oft teilen wir die beiden? Natürlich.
log(n)♪ So wird die Höhe unseres Baumes nicht mehr sein.
log(n)und auf jeder Ebene nicht mehr
n Gipfel, also endgültige Asymptomie
O(nlogn)♪
Jetzt müssen wir unsere Bedeutungen im Baum ändern. Sie können dies manuell tun, nur auf eine selektive Weise, um den Baum zu gehen, und wenn es um das Blatt geht, können Sie ein Element in die Masse setzen, und wenn wir wieder in das Feld, können Sie die Funktion an der aktuellen Spitze zählen.
Code
// v = aktuelles Top,
// d ist der zu addierende Elementindex,
/ d - zu ergänzen
Leere Veränderung(Node* v, int ind, int d) {~}
wenn (v-ferrb À= ind ) v-ferlb Artikel ind)
{~}
/ wenn wir zu der Spitze von
// Es gibt kein Element mit einer Nummer ind, dann gibt es keinen Punkt weiter.
zurück;
♪
wenn (v-tarlb + 1 == sync, berichtigt von elderman == @elder_man
{~}
/ Wenn wir das Blatt erreichen, fügen wir zu seinem Wert d
/ und Ende
v-nationalsum += d;
zurück;
♪
ändern(v-nationallinks, ind, d); /
ändern(v-nationalright, ind, d); //
v-nationalsum = v-stateleft-statesum + v-statright-statesum; // recount von Funktionen von Kindern
♪Asymptotisch wird gleich sein.
log(n)da die Höhe nicht größer ist
log(n)♪
Versuchen wir, eine Massenzugabe auf dem Boden zu machen.
[l;r) für Asymptotik
log(n)♪ Dann können wir zu einem Element als Massenzusatz auf der Länge eines hinzufügen. Das brauchen wir.
add♪ Wir werden Folgendes tun: Wir haben einen Antrag auf Hinzufügung auf dem Boden.
[l;r) Anzahl
d♪ Gehen wir nicht ehrlich und fügen Sie die Nummer auf dem Boden.
d, Erinnern wir uns nur daran, dass wir hinzufügen müssen. Feld
add und wird für dieses Gedächtnis verantwortlich sein.
Zunächst gibt es eine Funktion, die " ermutigen " Informationen über die Kinder ' s Ergänzung zur Spitze. Denn wenn unser aktuelles Top etwas hinzuzufügen braucht, müssen ihre Kinder genau das gleiche hinzufügen. In derselben Verantwortung werden wir die Funktion aller Unterstützung neu kalibrieren. Es ist ziemlich offensichtlich. Wie wird sich die Menge an der Größe ändern
sizewenn alle Elemente der gleichen Anzahl hinzugefügt werden
d? Es macht Sinn, dass es dir besser geht.
d*size♪ Wenn wir den Betrag nicht berücksichtigten, würde die Neuberechnung auf der Funktion basieren. Zum Beispiel, wenn es ein Minimum, würde es einfach eine Zahl auf ein Minimum hinzufügen.
d♪
Code
Leertaste(Node* v)
{~}
wenn (v)
{~}
// Wenn wir in der Spaltspitze sind,
♪ there's nowhere to push ♪
/ also tu einfach nichts
zurück;
♪
v-nationalsum += v-stateadd * (v-tarrb-v-lb); / Recosting of function
v-nationalleft-stateadd += v-stateadd; // Informationen zum linken Kind verschieben
v-nationalright-stateadd += v-stateadd; /// nach rechts schieben
v-nationaladd = 0; // wir haben bereits das aktuelle Top aktualisiert, so dass wir uns nicht mehr erinnern müssen.
♪Jetzt nehme ich die Additivfunktion auf den Schnitt:
Leere Veränderung(Node* v, int l, int r, int d)
{~}
push(v); // Push-Informationen
wenn (v-ferlb grad= r ) v- Bestandteil b À= l)
{~}
/ wenn die Schnitte unserer Oberseite und der Schnitt
/ schneidet sich, dann gibt es keinen Sinn zu gehen,
/ Weil sich nichts ändert
zurück;
♪
wenn (l PER= v-nationallb < r)
{~}
// wenn der Schnitt unserer Oberseite
/ liegt in der Anfrage, wir müssen die Bedeutungen ändern
/ in allen Unterstützung
v-nationaladd += d;
Push(v)
zurück;
♪
/ Wenn die ersten beiden Bedingungen nicht erfüllt sind,
- Ja.
Änderung(v-nationallinks, l, r, d);
Änderungen (v-nationalright, l, r, d);
wenn (v)
{~}
zurück;
♪
v-nationalsum = v-stateleft-statesum + v-statright-statesum; // Neuberechnung der Funktion von Kindern
♪Asymptomie dieser Funktion
O(logn)♪