runter.SPARSE TABELLE (entwickelte Tabelle) Sparse Table ist eine Datenstruktur, die auf Abfragen vom Typ " reagiert; den Wert der Funktion auf einem nicht ersetzbaren [L;R] " , mit O(1) Zeit und O(n*logn) Speicher finden, wobei n die Größe der Masse ist.
Ersatztabelle (nachfolgend " ST " ) wird nur mit impotenten Funktionen korrekt betrieben*
Strukturbeschreibung:
Bevor die ST selbst betrachtet wird, werden wir eine gewisse Tatsache betrachten, auf der die gesamte Bedeutung von ST beruht.
" Die Schnitte jeder Länge können durch zwei Schnitte abgedeckt werden, deren Länge die Stufen des Doppels sind und die Länge des zu bedeckenden Schnitts nicht überschreiten; (kann es selbst beweisen oder einfach glauben, dass es wahr ist).
Beispiele:

Was ist die Idee von ST: Lassen Sie uns die notwendige Funktion in der Masse auf allen Unterabschnitten vorhersagen, deren Länge die Doppelstufen ist und diese weiterhin verwenden, um auf Anfragen zu reagieren.
Es kann darauf hingewiesen werden, dass einige Sublets zweimal geschlossen werden. Deshalb arbeitet ST nur mit den impotenten Funktionen.
ST:
Kann F() die Funktion sein, die wir als im richtigen Bereich betrachten.
Wir haben d[logn][n], wo n die Größe der Masse ist.
d[i][j] - F() im Unterabschnitt der Bezugsmasse, deren Länge 2^i beträgt und in j beginnt.
Offensichtlich kennen wir die F() für die 2 ^0 Längen-Teilchen. 1 ist die Bedeutung der Masse.
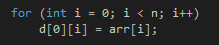
Wir berechnen dann die Werte wie folgt:
Kennen wir jetzt die F(s) für die Länge von 2^i. Wir haben bereits die Werte für die Längen von 2^(i-1) und 2^i = 2 *(i - 1) berechnet, so haben wir genug, um die F() der bereits berechneten Werte der beiden aufeinanderfolgenden Teilstellen von 2^(i-1) aus der aktuellen Position zu nehmen.
Zum Beispiel:
Wir zählen F() in einem Teilabschnitt der Länge 2 ab Position 0. Wir kennen bereits alle Werte auf allen Schnitten der Länge 1. Es genügt daher, F() von einem Schnitt der Länge 1, beginnend in Position 0 und einem Schnitt der Länge 1, beginnend in Punkt 1. Das ist, was das F() Paar in Position 0 beginnt. Ich meine, für jedes Paar betrachten wir zwei aufeinander folgende Einzelelemente, für jedes Quartal, zwei aufeinander folgende Paare, etc.
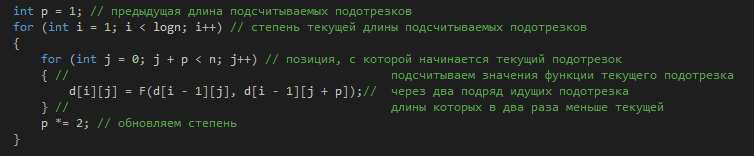
Baugewerbe - O(n*logn).
Antwort auf die Anfrage:
Mögen wir einen Antrag auf einen Schnitt [L;R] haben. Die erste Frage, die in den Sinn kommt: Welche Länge braucht es, um den Strom zu schließen? Wir müssen eine Zahl herausfinden, die das maximale Doppelte ist und die Länge der Anfrage nicht überschreitet. Um bei der Berechnung dieses Wertes nicht zu viel Zeit zu verschwenden, werden wir diesen Werten vorangehen, bevor wir auf Anfragen antworten.
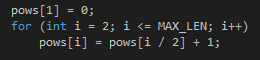
Wir machen eine Pows Masse... [MAX_LEN] wo MAX_LEN die maximale Länge einer möglichen Anfrage ist.
pows[i] - Zahl, die
2^Pows[i] Ø= i À À ^(pows[i] + 1).
Für jede Zahl (wirklich für jede mögliche Länge des Antrags) werden wir das maximale Doppel, das ist 2 in diesem Maße nicht mehr als die aktuelle Zahl.
Berechnung der Pows:
Wir haben die notwendige Länge, ihren Grad, der als der Wert der Funktionen auf der Masse für alle Teilabschnitte aller Stufen betrachtet wird. Es ist weiter relativ verständlich, dass wir das von der Abkürzung einer bestimmten Länge gezählte Gewicht nehmen, das an der L(Feldgrenze des Antrags) beginnt, den Wert aus der Abschaltung einer bestimmten Länge, die in der R(rechts Grenze des Antrags) endet und von ihnen F() zurückzieht. Das ist die Antwort. Da wir nur ST für impotente Operationen verwenden, ist die doppelte Überlappung einiger Fragmente nicht beängstigend.

*Over impotent:
Hypothetismus ist die Art des Objekts oder der Operation, wenn die Operation wieder in die Anlage verwendet wird, um das gleiche Ergebnis wie die zu erzeugen.
Formal, F ist maßgebend, wenn F(x;x) = x durchgeführt wird;
Min(5, 5) = 5 - konstant min - impotent funktion
Summe(5; 5) = 10 - Volumen nicht verfügbar
Häufig in den Aufgaben der imputierten Operationen eingesetzt: min, max, gcd (NOD).