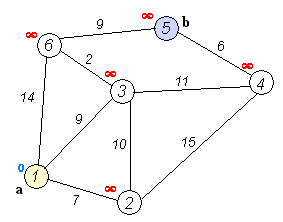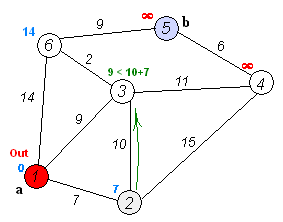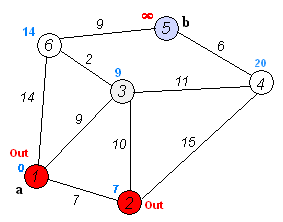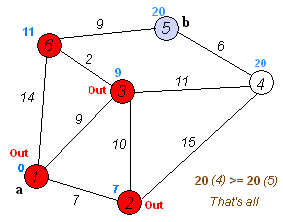
Dado un gráfico ponderado dirigido o no dirigido con n vértices y m aristas. Los pesos de todos los bordes no son negativos. Se especifica algún vértice inicial. Debe encontrar las longitudes de las rutas más cortas desde el vértice s hasta todos los demás vértices, y también proporcionar una forma de imprimir las rutas más cortas.
Este problema se denomina "problema de ruta más corta de fuente única" (problema de rutas más cortas de fuente única).
Realiza las mismas tareas que 1-K BFS, pero sin tener en cuenta K. Además, como 1-K BFS, no maneja adecuadamente los bordes negativos
Algoritmo:
El propio algoritmo de Dijkstra consta de N iteraciones. En la siguiente iteración, el vértice V con la distancia más pequeña a él de entre los vértices aún no marcados, este vértice se marca y se producen relajaciones de los vértices vecinos a partir de él.
el comportamiento asintótico final del algoritmo es: O(n
2+ m)