به جای اینکه فقط هش یک دنباله را محاسبه کنیم، می توانیم مقدار را در هر یک از پیشوندهای آن ذخیره کنیم. توجه داشته باشید که اینها مقادیر هش برای دنباله هایی برابر با پیشوند مربوطه خواهند بود.
با چنین ساختاری، می توانید به سرعت مقدار هش را برای هر زیربخشی از این دنباله (شبیه به جمع پیشوندها) محاسبه کنید.
اگر بخواهیم هش زیربخش [l;r] را محاسبه کنیم، باید هش پیشوند r را بگیریم و هش پیشوند l-1 را در p ضرب کنیم به توان r-l+1. اگر این مقادیر را روی پیشوندها بنویسید و ببینید چه اتفاقی میافتد، دلیل این امر مشخص میشود. امیدوارم با دیدن این عکس موفق باشید.
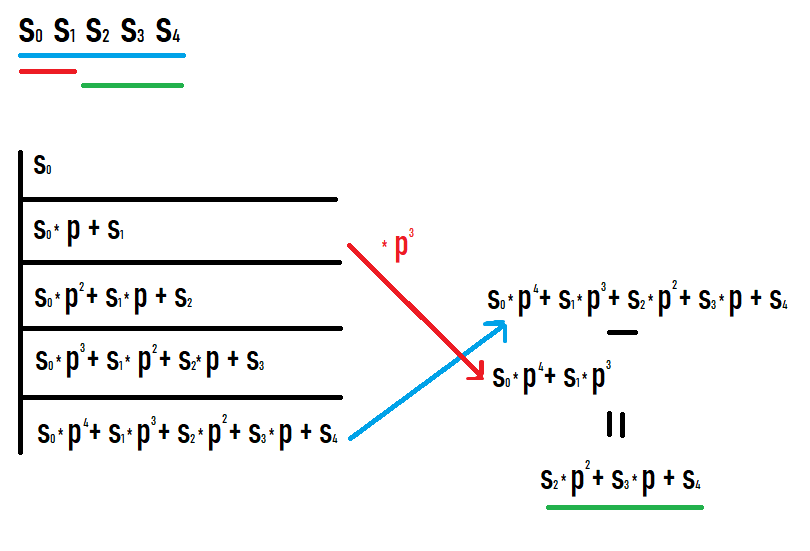
در نتیجه چنین اقداماتی، یک هش از یک زیربخش از دنباله اصلی دریافت می کنیم. علاوه بر این، این هش برابر با آن است که به عنوان هش از دنباله ای برابر با این زیربخش در نظر گرفته شود (برای مقایسه با مقادیر دیگر نیازی به تبدیل اضافی درجه یا موارد مشابه نیست).
در اینجا دو نکته قابل توضیح است:
1) برای ضرب سریع p در توان r-l+1، لازم است تمام توان های ممکن مدول p modulo از قبل محاسبه شود.
2) باید به خاطر داشت که ما همه محاسبات مدول مدول را انجام می دهیم و بنابراین ممکن است معلوم شود که پس از کم کردن هش های پیشوند، یک عدد منفی به دست می آوریم. برای جلوگیری از این امر، همیشه میتوانید مد را قبل از تفریق اضافه کنید. همچنین فراموش نکنید که مقدار مدول را بعد از ضرب و همه جمع ها بگیرید.
در کد به صورت زیر است:
#include <bits/stdc++.h>
با استفاده از namespace std.
typedef long longll;
const int MAXN = 1000003;
// ماژول پایه و هش
ll p، mod;
// پیشوند هش و توان p
h[MAXN]، pows[MAXN]؛
// محاسبه هش زیربخش [l;r]
ll get_segment_hash(int l, int r) {
بازگشت (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod;
}
int main()
{
// به نوعی p و mod را دریافت کنید
// پیش محاسبه توان ها ص
pows[0] = 1;
برای (int i = 0; i < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod;
//
// راه حل اصلی مشکل
//
بازگشت 0;
}