Problem
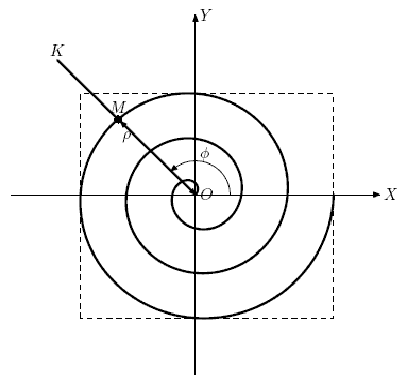
دیما اخیراً به موسسه تحقیقاتی منحنی های مسطح پیوسته است. همانطور که از نام این پژوهشکده پیداست در زمینه منحنی های صفحه به تحقیقات مختلفی می پردازد. اخیراً گئورگی رئیس دیمین با منحنی بسیار جالبی روبرو شد که همانطور که پس از تحقیقات مشخص شد به مارپیچ ارشمیدسی معروف است. مارپیچ ارشمیدسی منحنی صفحه ای است که مسیر نقطه M را نشان می دهد که به طور یکنواخت در امتداد پرتو OK با مبدأ در O حرکت می کند، در حالی که خود پرتو OK به طور یکنواخت در اطراف نقطه O می چرخد (شکل را ببینید). به عبارت دیگر فاصله تا مبدا ρ = OM به طور خطی به زاویه چرخش .phi وابسته است. پرتو خوب است در این حالت، چرخش پرتو OK با همان زاویه مطابق با افزایش فاصله یکسان ρ.
حرکت نقطه M را می توان با استفاده از تعدادی پارامتر تنظیم کرد:
• زاویه اولیه چرخش آلفا. پرتو OK (بر حسب درجه در خلاف جهت عقربه های ساعت نسبت به جهت مثبت محور OX اندازه گیری می شود)؛
• سرعت زاویه ای .omega. ray OK (برحسب درجه در واحد زمان اندازه گیری می شود)؛
• فاصله اولیه R از نقطه M تا مبدا (نقطه O)؛
• سرعت V نقطه M در امتداد پرتو OK.
اگر با تنظیم این پارامترها، زمان حرکت نقطه M را محدود نکنیم، منحنی بی نهایت به دست می آید که کشف آن بسیار دشوار است. بنابراین، دیما تصمیم گرفت خود را به مطالعه بخشی از این منحنی محدود کند، منحنی که وقتی نقطه M از لحظه صفر زمان به لحظه T حرکت می کند، به دست می آید. مشکلی که دیما حل می کند یافتن مستطیلی از زمان است حداقل مساحت با اضلاع موازی با محورهای مختصات، که در آن می توان آن را درج کرد.
باید برنامه ای بنویسید که مستطیل مورد نظر را پیدا کند
ورودی
فایل ورودی شامل چهار عدد صحیح است: ω (1 ≤ امگا؛ ≤ 100)، V (1 ≤ V ≤ 100)، R (0 ≤ R ≤ 100) و T (1 ≤ T ≤ 1000). در این مشکل، فرض می شود که زاویه چرخش اولیه .alpha است. صفر است.
خروجی
در خط اول فایل خروجی دو عدد واقعی — مختصات گوشه سمت چپ پایین مستطیل مورد نظر و در خط دوم — مختصات گوشه سمت راست بالای مستطیل مورد نظر.
اگر مقدار هر یک از مختصات با مقدار واقعی بیش از 10-5 تفاوت نداشته باشد، پاسخ صحیح تلقی می شود.
<بدن>
| ورودی |
خروجی |
| 60 10 0 18 |
-150.3028434716 -165.2754877824
180.0000000000 135.3362037333
|
المپیاد تیمی، VKOSHP، 2008، مسئله I