ترکیب n عنصر توسط k ترکیباتی هستند که می توانند از n عنصر تشکیل شوند و k عنصر را در هر اتصال جمع آوری کنند. در حالی که اتصالات فقط توسط خود عناصر با یکدیگر تفاوت دارند (تفاوت در ترتیب چیدمان آنها در نظر گرفته نشده است).
برای مثال، ترکیب های زیر را می توان از 3 عنصر (a,b,c)(a,b,c) 2 هر کدام تشکیل داد: ab,ac,bc.
تعداد همه ترکیبهای ممکنی که میتوانند از n عنصر با k تشکیل شوند با علامت
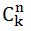
و با فرمول:
محاسبه می شود
دو راه برای یافتن تعداد ترکیب ها وجود دارد
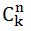
1. n!، k!، (n – k) را پیدا کنید! و طبق فرمول بالا مقدار را محاسبه می کنیم اما از – به دلیل سرریز احتمالی، این روش را می توان با n <= 12 استفاده کرد.
2. با برنامه نویسی پویا.
DP شبیه مثلث پاسکال خواهد بود که در بالا و لبهها قرار دارند و هر عدد برابر است با مجموع دو عدد بالای آن.
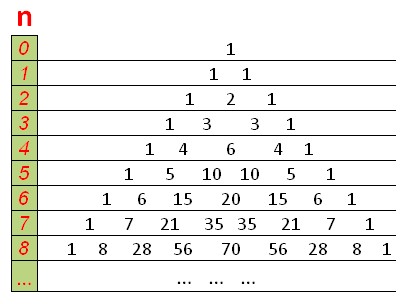
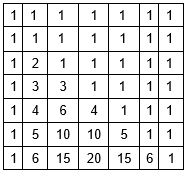
تابعی که تعداد ترکیب ها را با استفاده از برنامه نویسی پویا در O(n^2) می شمارد:
ایجاد شد
int C(int n، int دهانه > k)
{
بردار<بردار<int> > dp(n + 1، vector<int>(n + 1, 1)); // ایجاد یک آرایه dp با اندازه (n + 1، n + 1)
برای (int i = 0; i <= n; i++) // خط i-ام آرایه را پر کنید
{
برای (int j = 1; j < i; j++)
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; //محاسبه مجدد موقعیت (i;j) از طریق (i - 1; j - 1) و (i - 1; j)
}
}
بازگشت dp[n][k]; //return value
}