Les combinaisons de n éléments par k sont des composés qui peuvent être formés à partir de n éléments, rassemblant k éléments dans chaque connexion ; tandis que les connexions ne diffèrent les unes des autres que par les éléments eux-mêmes (la différence dans l'ordre de leur disposition n'est pas prise en compte).
Par exemple, les combinaisons suivantes peuvent être formées à partir de 3 éléments (a,b,c)(a,b,c) 2 chacun : ab,ac,bc.
Le nombre de toutes les combinaisons possibles pouvant être formées à partir de n éléments par k est indiqué par le symbole
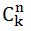
et calculé par la formule :
;
Il existe deux façons de trouver le nombre de combinaisons
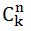
1. Trouvez n!, k!, (n – k) ! et selon la formule ci-dessus, on calcule la quantité, mais à partir de – en raison d'un éventuel débordement, cette méthode peut être utilisée avec n <= 12.
2. Avec programmation dynamique.
Le DP ressemblera au triangle de Pascal, avec des uns en haut et sur les bords, et chaque nombre est égal à la somme des deux nombres au-dessus.
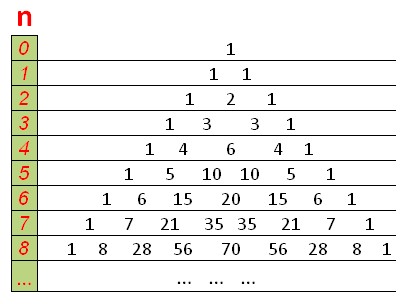
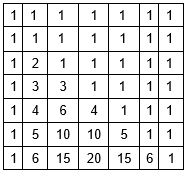
Une fonction qui compte le nombre de combinaisons en utilisant la programmation dynamique en O(n ^2 ) :
int C(int n, int k)
{
vecteur<vecteur<int> ; > dp(n + 1, vecteur<int>(n + 1, 1)); // Créer un tableau dp de taille (n + 1, n + 1)
pour (int i = 0 ; i <= n ; i++) // Remplissez la ième ligne du tableau
{
pour (int j = 1 ; j < i ; j++)
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] ; //recalculer la position (i;j) à travers (i - 1; j - 1) et (i - 1; j)
}
}
retour dp[n][k] ; //valeur de retour
}