Problem
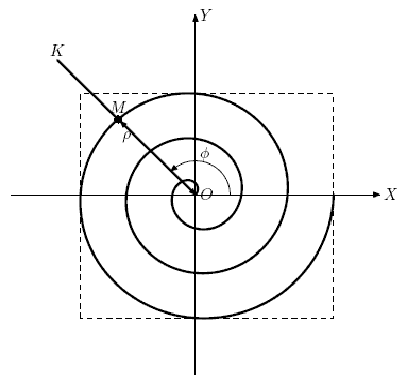
Dima a récemment rejoint l'Institut de recherche sur les courbes plates. Comme le nom de cet institut de recherche l'indique, il est engagé dans diverses recherches dans le domaine des courbes planes. Récemment, le patron de Dimin, Georgy, a rencontré une courbe très intéressante qui, après quelques recherches, est connue sous le nom de spirale d'Archimède. La spirale d'Archimède est une courbe plane représentant la trajectoire du point M, qui se déplace uniformément le long du rayon OK avec l'origine en O, tandis que le rayon OK lui-même tourne uniformément autour du point O (voir figure). En d'autres termes, la distance à l'origine ρ = OM dépendant linéairement de l'angle de rotation .phi. faisceau OK. Dans ce cas, la rotation du rayon OK du même angle correspond au même incrément de distance ρ.
Le mouvement du point M peut être défini à l'aide de plusieurs paramètres :
• angle de rotation initial .alpha. faisceau OK (mesuré en degrés dans le sens antihoraire par rapport à la direction positive de l'axe OX) ;
• vitesse angulaire .omega. rayon OK (mesuré en degrés par unité de temps);
• la distance initiale R du point M à l'origine (point O) ;
• vitesse V du point M le long du rayon OK.
Si, en fixant ces paramètres, on ne limite pas le temps de déplacement du point M, alors on obtient une courbe infinie, assez difficile à explorer. Par conséquent, Dima a décidé de se limiter à étudier une partie de cette courbe, celle qui est obtenue lorsque le point M passe de l'instant zéro à l'instant T. Le problème que Dima résout est de trouver un rectangle du zone minimale avec des côtés parallèles aux axes de coordonnées, dans laquelle il peut être inscrit.
Vous devez écrire un programme qui trouvera le rectangle souhaité
Entrée
Le fichier d'entrée contient quatre entiers : ω (1 ≤ oméga; ≤ 100), V (1 ≤ V ≤ 100), R (0 ≤ R ≤ 100) et T (1 ≤ T ≤ 1000). Dans ce problème, on suppose que l'angle de rotation initial .alpha. est zéro.
Sortie
Dans la première ligne du fichier de sortie, imprimez deux nombres réels — les coordonnées du coin inférieur gauche du rectangle souhaité, et en seconde ligne — coordonnées du coin supérieur droit du rectangle souhaité.
La réponse sera considérée comme correcte si la valeur de chacune des coordonnées ne diffère pas de la vraie valeur de plus de 10-5.
| Entrée |
Sortie |
| 60 10 0 18 |
-150.3028434716 -165.2754877824
180.0000000000 135.3362037333
Olympiade par équipe, VKOSHP, 2008, Problème I