Problem
Une araignée et une araignée flottent sur le lac sur deux branches. Ils ne savent pas nager, ils ne peuvent donc se rencontrer que lorsque les branches se touchent.
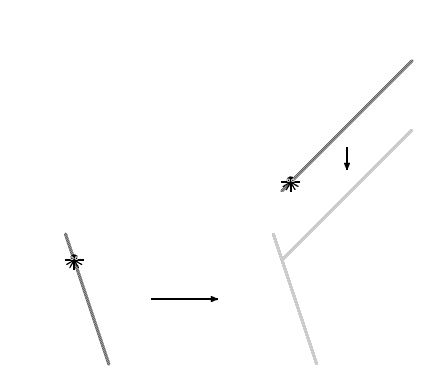
En supposant que des branches sont en forme de segments, et qu'ils nagent à des vitesses constantes, déterminez combien de temps il faut pour rencontrer le malheureux arthropode.
Entrée
Le fichier d'entrée contient 12 nombres : x1, y1, x2, y2, x 3, y3, x4, y4, v1x, v 1y, v2x, v2y. Les coordonnées des sommets du premier segment : (x1, y1) et (x2, y2 sub>), coordonne les sommets du deuxième segment : (x3, y3) et (x4, y4< /sub>), la vitesse du premier segment (v1x, v1y), la vitesse du second segment (v2x, v2y). Tous les nombres sont des nombres entiers et ne dépassent pas 104 en valeur absolue.Au moment initial, les branches ne se touchent pas. Les branches sont garanties d'avoir une longueur non nulle.
Sortie
Sortir dans le fichier de sortie le temps jusqu'au moment le plus proche où les branches se touchent, avec une erreur ne dépassant pas 10
−4. Si les branches ne se touchent jamais, imprimez le chiffre -1.
| Entrée |
Sortie |
0 0 -1 3
4 4 7 7
3 0
0 -1
1.6 |
0 0 -1 3
4 4 7 7
10
0 -3
-1 |
Olympiades par équipe, Championnats de programmation par équipe des écoliers de Saint-Pétersbourg, 2006, Problème E