Hachage

Error

Au lieu de simplement calculer le hachage d'une séquence, nous pouvons stocker la valeur à chacun de ses préfixes. Notez qu'il s'agira de valeurs de hachage pour les séquences égales au préfixe correspondant.

Avec une telle structure, vous pouvez rapidement calculer la valeur de hachage pour n'importe quel sous-segment de cette séquence (similaire aux sommes de préfixes).

Si nous voulons calculer le hachage du sous-segment [l;r], alors nous devons prendre le hachage sur le préfixe r et soustraire le hachage sur le préfixe l-1 multiplié par p à la puissance r-l+1. Pourquoi il en est ainsi devient clair si vous écrivez les valeurs sur les préfixes et voyez ce qui se passe. J'espère que vous réussirez à regarder cette photo.



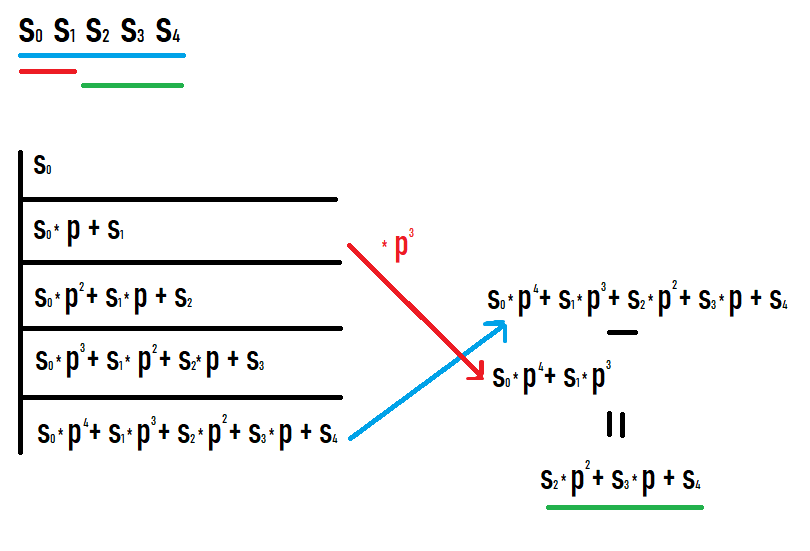
À la suite de telles actions, nous obtenons un hachage d'un sous-segment de la séquence d'origine. De plus, ce hachage est égal à celui s'il était considéré comme un hachage d'une séquence égale à ce sous-segment (aucune conversion supplémentaire de degrés ou similaire n'est requise pour comparer avec d'autres valeurs).

Il y a deux points à clarifier ici :
1) Pour multiplier rapidement par p à la puissance r-l+1, il faut précalculer toutes les puissances possibles de p modulo mod.
2) Il faut se rappeler que nous effectuons tous les calculs modulo modulo, et donc il peut s'avérer qu'après avoir soustrait les hachages de préfixe, nous obtiendrons un nombre négatif. Pour éviter cela, vous pouvez toujours ajouter un mod avant de soustraire. Aussi, n'oubliez pas de prendre la valeur modulo après multiplications et toutes additions.

Dans le code, cela ressemble à ceci :
  #include <bits/stdc++.h> en utilisant l'espace de noms std ; typedef long longll ; const entier MAXN = 1000003 ; // module de base et de hachage ll p, mod; // préfixe hachage et exposants p h[MAXN], pows[MAXN] ; // calcul du hash du sous-segment [l;r] ll get_segment_hash(int l, int r) { retour (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod ; } int main() { // obtenir en quelque sorte p et mod // précalcule les puissances p pows[0] = 1 ; pour (int i = 0; je < MAXN; i++) pows[i] = (pows[i - 1] * p) % mod ; // // solution du problème principal // renvoie 0 ; }

Si nous avons un hachage de la chaîne A égal à h_A et un hachage de la chaîne B égal à h_B, alors nous pouvons rapidement calculer le hachage de la chaîne AB :
h_AB = h_A * p^|B| + h_B   <- tout compter modulo
où |B| - la longueur de la chaîne B.

En plus des séquences, vous pouvez également hacher des ensembles. C'est-à-dire des ensembles d'objets sans ordre. Il est calculé selon la formule suivante :
hachage(A) = \(\sum_{a \in A} p^{ord(a)}\)   <- tout compter modulo
où ord est une fonction qui attribue à un objet de l'ensemble son nombre ordinal absolu parmi tous les objets possibles (par exemple, si les objets sont des nombres naturels, alors ord(x) = x, et si des lettres latines minuscules, alors ord(& #39;a' ;) = 1, ord('b') = 2 etc.)

C'est-à-dire que pour chaque objet on associe une valeur égale à la base à la puissance du nombre de cet objet et on additionne toutes ces valeurs afin d'obtenir un hachage de l'ensemble entier. Comme il ressort clairement de la formule, le hachage est facilement recalculé si un élément est ajouté ou supprimé de l'ensemble (il suffit d'ajouter ou de soustraire la valeur requise). Même logique,  si ce ne sont pas des éléments uniques qui sont ajoutés ou supprimés, mais d'autres ensembles (il suffit d'ajouter/soustraire leur hachage).

Comme vous pouvez déjà le comprendre, les éléments simples sont considérés comme des ensembles de taille 1, pour lesquels nous pouvons calculer le hachage. Et les ensembles plus grands ne sont qu'une union de ces ensembles uniques, où en combinant des ensembles, nous ajoutons leurs hachages.

En fait, c'est toujours le même hachage polynomial, mais avant le coefficient à p^m  nous avions la valeur de l'élément de séquence sous le numéro n - m - 1 (où n est la longueur de la séquence), et maintenant c'est le nombre d'éléments dans l'ensemble dont le nombre ordinal absolu est égal à m.

Dans un tel hachage, il faut prendre une base suffisamment grande (supérieure à la taille maximale de l'ensemble), ou utiliser un double hachage pour éviter les situations où un ensemble de p objets de nombre ordinal absolu m a le même hachage qu'un ensemble à un objet avec un nombre ordinal absolu m+1.
 

Il existe également plusieurs façons de hacher efficacement les arbres enracinés. 
L'une de ces méthodes est organisée comme suit :
Nous traitons les sommets de manière récursive, dans l'ordre de parcours en profondeur. Nous supposerons que le hachage d'un seul sommet est égal à p. Pour les sommets avec des enfants, nous exécutons d'abord l'algorithme pour eux, puis à travers les enfants, nous calculerons le hachage du sous-arbre actuel. Pour ce faire, considérez les hachages des sous-arbres d'enfants comme une séquence de nombres et calculez le hachage à partir de cette séquence. Ce sera le hachage du sous-arbre actuel.
Si l'ordre des enfants n'est pas important pour nous, alors avant de calculer le hachage, nous trions la séquence de hachages des sous-arbres enfants, puis calculons le hachage à partir de la séquence triée.

De cette façon, vous pouvez vérifier l'isomorphisme des arbres - il suffit de compter le hachage sans ordre sur les enfants (c'est-à-dire de trier à chaque fois les hachages des enfants). Et si les hachages des racines correspondent, alors les arbres sont isomorphes, sinon non.

Pour les arbres non enracinés, tout se passe de la même manière, mais le centroïde doit être pris comme racine. Ou considérez une paire de hachages s'il y a deux centroïdes.