Le combinazioni di n elementi per k sono composti che possono essere formati da n elementi, raccogliendo k elementi in ogni connessione; mentre le connessioni differiscono l'una dall'altra solo per gli elementi stessi (la differenza nell'ordine della loro disposizione non viene presa in considerazione).
Ad esempio, le seguenti combinazioni possono essere formate da 3 elementi (a,b,c)(a,b,c) 2 ciascuno: ab,ac,bc.
Il numero di tutte le possibili combinazioni che si possono formare da n elementi per k è indicato dal simbolo
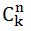
e calcolato con la formula:
Esistono due modi per trovare il numero di combinazioni
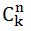
1. Trova n!, k!, (n – k)! e secondo la formula sopra, calcoliamo la quantità, ma da – a causa del possibile overflow, questo metodo può essere utilizzato con n <= 12.
2. Con la programmazione dinamica.
Il DP assomiglierà al triangolo di Pascal, con uno in alto e ai bordi, e ogni numero è uguale alla somma dei due numeri sopra di esso.
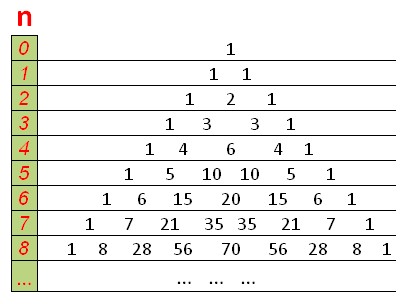
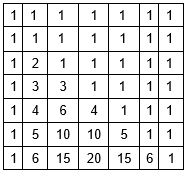
Una funzione che conta il numero di combinazioni utilizzando la programmazione dinamica in O(n ^2 ):
int C(int n, int k)
{
vettore<vettore<int> > dp(n + 1, vettore<int>(n + 1, 1)); // Crea un array dp di dimensione (n + 1, n + 1)
for (int i = 0; i <= n; i++) // Compila la i-esima riga dell'array
{
for (int j = 1; j < i; j++)
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; //ricalcolo della posizione (i;j) tramite (i - 1; j - 1) e (i - 1; j)
}
}
ritorno dp[n][k]; //valore restituito
}