Hashing

Error

Invece di calcolare semplicemente l'hash di una sequenza, possiamo memorizzare il valore in ciascuno dei suoi prefissi. Si noti che questi saranno valori hash per sequenze uguali al prefisso corrispondente.

Con una tale struttura, puoi calcolare rapidamente il valore hash per qualsiasi sottosegmento di questa sequenza (simile alle somme dei prefissi).

Se vogliamo calcolare l'hash del sottosegmento [l;r], allora dobbiamo prendere l'hash sul prefisso r e sottrarre l'hash sul prefisso l-1 moltiplicato per p alla potenza di r-l+1. Perché è così diventa chiaro se scrivi i valori sui prefissi e vedi cosa succede. Spero che tu riesca a guardare questa foto.



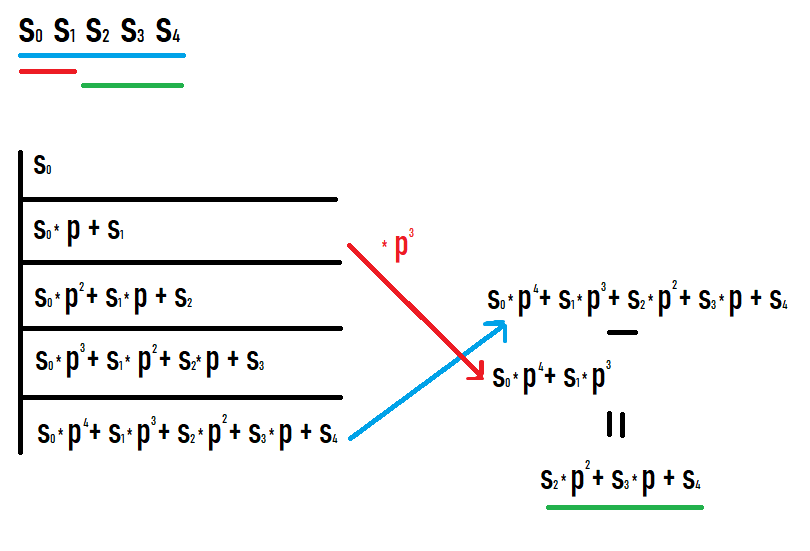
Come risultato di tali azioni, otteniamo un hash di un sottosegmento della sequenza originale. Inoltre, questo hash è uguale a quello se fosse considerato come un hash da una sequenza uguale a questo sottosegmento (non sono necessarie ulteriori conversioni di gradi o simili per il confronto con altri valori).

Ci sono due punti da chiarire qui:
1) Per moltiplicare velocemente per p alla potenza r-l+1, è necessario precalcolare tutte le potenze possibili di p modulo mod.
2) Va ricordato che eseguiamo tutti i calcoli modulo modulo, e quindi potrebbe risultare che dopo aver sottratto gli hash del prefisso, otterremo un numero negativo. Per evitare ciò, puoi sempre aggiungere mod prima di sottrarre. Inoltre, non dimenticare di prendere il valore del modulo dopo le moltiplicazioni e tutte le addizioni.

Nel codice ha questo aspetto:
  #include <bits/stdc++.h> utilizzando lo spazio dei nomi std; typedef long longll; const int MAXN = 1000003; // modulo base e hash ll p, mod; // prefisso hash ed esponenti p h[MAXN], pots[MAXN]; // calcolo dell'hash del sottosegmento [l;r] ll get_segment_hash(int l, int r) { return (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod; } int principale() { // in qualche modo ottieni p e mod // precalcola le potenze p pot[0] = 1; for (int i = 0; i < MAXN; i++) pows[i] = (pows[i - 1] * p) % mod; // // soluzione del problema principale // ritorno 0; }

Se abbiamo un hash della stringa A uguale a h_A e un hash della stringa B uguale a h_B, allora possiamo calcolare velocemente l'hash della stringa AB:
h_AB = h_A * p^|B| + h_B   <- contare tutto modulo
dove |B| - la lunghezza della corda B.

Oltre alle sequenze, puoi anche hash set. Cioè, insiemi di oggetti senza ordine su di essi. Viene calcolato secondo la seguente formula:
hash(A) = \(\sum_{a \in A} p^{ord(a)}\)   <- contare tutto modulo
dove ord è una funzione che assegna ad un oggetto dell'insieme il suo numero ordinale assoluto tra tutti i possibili oggetti (per esempio, se gli oggetti sono numeri naturali, allora ord(x) = x, e se lettere latine minuscole, allora ord(& #39;a' ;) = 1, ord('b') = 2 ecc.)

Cioè, per ogni oggetto associamo un valore pari alla base alla potenza del numero di questo oggetto e sommiamo tutti questi valori per ottenere un hash dell'intero insieme. Come risulta chiaro dalla formula, l'hash viene facilmente ricalcolato se un elemento viene aggiunto o rimosso dall'insieme (basta aggiungere o sottrarre il valore richiesto). Stessa logica,  se non vengono aggiunti o rimossi singoli elementi, ma altri insiemi (basta aggiungere/sottrarre il loro hash).

Come puoi già capire, i singoli elementi sono considerati come insiemi di dimensione 1, per i quali possiamo calcolare l'hash. E i set più grandi sono semplicemente un'unione di tali set singoli, dove combinando i set, aggiungiamo i loro hash.

In effetti, questo è sempre lo stesso hash polinomiale, ma prima del coefficiente in p^m , avevamo il valore dell'elemento della sequenza sotto il numero n - m - 1 (dove n è la lunghezza della sequenza), e ora questo è il numero di elementi nell'insieme il cui numero ordinale assoluto è uguale a m.

In tale hashing, si deve prendere una base sufficientemente grande (maggiore della dimensione massima dell'insieme), o usare il doppio hashing per evitare situazioni in cui un insieme di p oggetti con numero ordinale assoluto m ha lo stesso hash di un insieme con un oggetto con numero ordinale assoluto m. numero ordinale m+1.
 

Esistono anche diversi modi per eseguire in modo efficiente l'hashing degli alberi radicati. 
Uno di questi metodi è organizzato come segue:
Elaboriamo i vertici in modo ricorsivo, in ordine di attraversamento in profondità. Supponiamo che l'hash di un singolo vertice sia uguale a p. Per i vertici con figli, prima eseguiamo l'algoritmo per loro, quindi attraverso i figli calcoleremo l'hash del sottoalbero corrente. Per fare ciò, considera gli hash dei sottoalberi dei figli come una sequenza di numeri e calcola l'hash da questa sequenza. Questo sarà l'hash del sottoalbero corrente.
Se l'ordine sui figli non è importante per noi, prima di calcolare l'hash, ordiniamo la sequenza di hash dai sottoalberi figli e quindi calcoliamo l'hash dalla sequenza ordinata.

In questo modo puoi controllare l'isomorfismo degli alberi: basta contare l'hash senza ordine sui figli (ovvero, ogni volta ordinando gli hash dei figli). E se gli hash delle radici corrispondono, allora gli alberi sono isomorfi, altrimenti no.

Per gli alberi senza radici, tutto avviene in modo simile, ma il baricentro deve essere preso come radice. Oppure considera una coppia di hash se ci sono due centroidi.