Problem
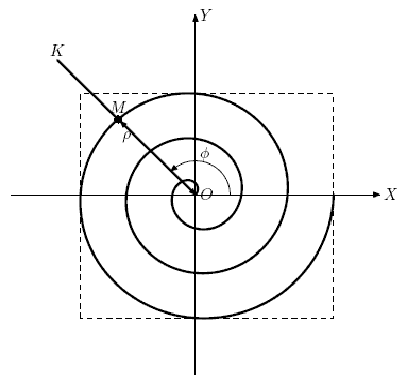
Dima は最近、フラット カーブ研究所に加わりました。この研究所の名前が示すように、平面曲線の分野でさまざまな研究を行っています。最近、Dimin の上司である Georgy は非常に興味深い曲線に遭遇しました。いくつかの調査の結果、アルキメデスの螺旋として知られていることが判明しました。アルキメデスのらせんは、点 M の軌跡を表す平面曲線であり、O を原点として光線 OK に沿って一様に移動しますが、光線 OK 自体は点 O の周りを一様に回転します (図を参照)。つまり、原点までの距離 ρ =OMは、回転角φに線形に依存する。ビームOK。この場合、光線 OK の同じ角度の回転は、同じ距離増分に対応します ρ.
ポイント M の移動は、いくつかのパラメーターを使用して設定できます:
•初期回転角αビーム OK (OX 軸の正の方向に対して反時計回りの角度で測定);
•角速度ω ray OK (単位時間あたりの角度で測定);
•点 M から原点 (点 O) までの初期距離 R;
•光線に沿った点 M の速度 V OK.
これらのパラメータを設定して、点 M の移動時間を制限しない場合、探索が非常に困難な無限曲線が得られます。したがって、Dima は、点 M がゼロの瞬間から瞬間 T に移動するときに得られるこの曲線の一部を研究することに専念することにしました。Dima が解決する問題は、次の長方形を見つけることです。内接できる座標軸に平行な辺を持つ最小領域。
目的の長方形を見つけるプログラムを作成する必要があります
入力
入力ファイルには 4 つの整数が含まれています。 (1 ≤ オメガ; ≤ 100)、V (1 ≤ V ≤ 100)、R (0 ≤ R ≤ 100)、および T (1 ≤ T ≤ 1000)。この問題では、初期の回転角度αが 1 であると仮定します。はゼロです。
出力
出力ファイルの最初の行に、2 つの実数を出力します —目的の四角形の左下隅の座標、および 2 行目 —目的の長方形の右上隅の座標。
各座標の値が真の値と 10-5 以内で異なる場合、答えは正しいと見なされます。
<本体>
| 入力 |
出力 |
| 60 10 0 18 |
-150.3028434716 -165.2754877824
180.0000000000 135.3362037333
|
チームオリンピアード、VKOSHP、2008 年、問題 I