Problem
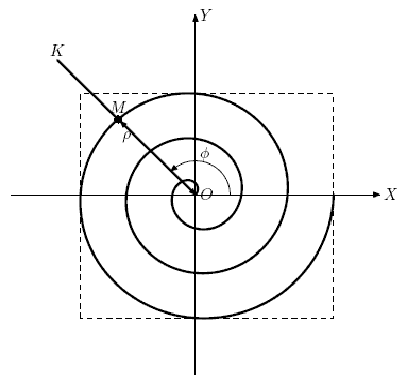
Dima는 최근 평평한 곡선 연구소에 합류했습니다. 이 연구소는 이름에서 알 수 있듯이 평면곡선 분야의 다양한 연구를 하고 있습니다. 최근 Dimin의 상사 Georgy는 아르키메데스 나선으로 알려진 매우 흥미로운 곡선을 발견했습니다. 아르키메데스 나선은 점 M의 궤적을 나타내는 평면 곡선입니다. 이 점은 O를 원점으로 하는 광선 OK를 따라 균일하게 이동하는 반면 광선 OK 자체는 점 O 주위를 균일하게 회전합니다(그림 참조). 즉, 원점까지의 거리 ρ = OM은 회전 각도 .phi에 선형적으로 의존합니다. 빔 확인. 이 경우 동일한 각도만큼 광선 OK의 회전은 동일한 거리 증분에 해당합니다.
지점 M의 이동은 여러 매개변수를 사용하여 설정할 수 있습니다.
&황소; 초기 회전 각도 .alpha. 빔 양호(OX 축의 양의 방향을 기준으로 시계 반대 방향으로 측정됨);
&황소; 각속도 .omega. ray OK(시간 단위당 각도로 측정);
&황소; 점 M에서 원점(점 O)까지의 초기 거리 R;
&황소; 광선을 따라 점 M의 속도 V OK.
이러한 매개 변수를 설정하여 점 M의 이동 시간을 제한하지 않으면 탐색하기 어려운 무한 곡선을 얻습니다. 따라서 Dima는 점 M이 시간의 0에서 시간 T로 이동할 때 얻어지는 이 곡선의 일부를 연구하는 것으로 자신을 제한하기로 결정했습니다. Dima가 해결하는 문제는 다음의 직사각형을 찾는 것입니다. 새겨질 수 있는 좌표축에 평행한 측면이 있는 최소 영역.
원하는 사각형을 찾는 프로그램을 작성해야 합니다.
입력
입력 파일에는 4개의 정수가 포함되어 있습니다. ω (1 < omega; < 100), V(1 < V < 100), R(0 < R < 100) 및 T(1 < T < 1000). 이 문제에서 초기 회전 각도는 .alpha라고 가정합니다. 0입니다.
출력
출력 파일의 첫 번째 줄에 두 개의 실수를 인쇄합니다. — 원하는 직사각형의 왼쪽 하단 모서리와 두 번째 줄의 좌표 — 원하는 사각형의 오른쪽 위 모서리 좌표.
각 좌표의 값이 실제 값과 10-5 이상 차이가 나지 않으면 정답으로 간주됩니다.
<몸>
| 입력 |
출력 |
| 60 10 0 18 |
-150.3028434716 -165.2754877824
180.0000000000 135.3362037333
|
팀 올림피아드, VKOSHP, 2008, 문제 I