Gabungan n unsur oleh k ialah sebatian yang boleh dibentuk daripada n unsur, mengumpul k unsur dalam setiap sambungan; manakala sambungan berbeza antara satu sama lain hanya oleh unsur-unsur itu sendiri (perbezaan dalam susunan susunannya tidak diambil kira).
Sebagai contoh, gabungan berikut boleh dibentuk daripada 3 unsur (a,b,c)(a,b,c) 2 setiap satu: ab,ac,bc.
Bilangan semua kemungkinan gabungan yang boleh dibentuk daripada n elemen dengan k ditunjukkan oleh simbol
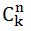
dan dikira dengan formula:
Terdapat dua cara untuk mencari bilangan gabungan
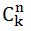
1. Cari n!, k!, (n – k)! dan mengikut formula di atas, kami mengira kuantiti, tetapi dari – disebabkan kemungkinan limpahan, kaedah ini boleh digunakan dengan n <= 12.
2. Dengan pengaturcaraan dinamik.
DP akan kelihatan seperti segi tiga Pascal, dengan satu di bahagian atas dan tepi, dan setiap nombor sama dengan jumlah dua nombor di atasnya.
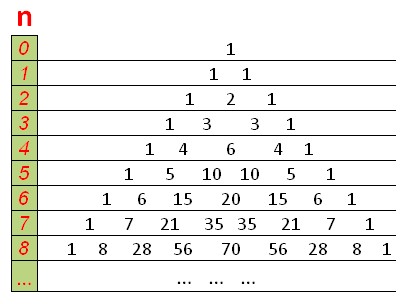
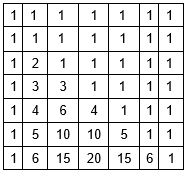
Fungsi yang mengira bilangan gabungan menggunakan pengaturcaraan dinamik dalam O(n ^2 ):
int C(int n, int k)
{
vektor<vektor<int> > dp(n + 1, vektor<int>(n + 1, 1)); // Buat tatasusunan dp saiz (n + 1, n + 1)
untuk (int i = 0; i <= n; i++) // Isikan baris ke-i tatasusunan
{
untuk (int j = 1; j < i; j++)
{
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; //mengira semula kedudukan (i;j) melalui (i - 1; j - 1) dan (i - 1; j)
}
}
kembali dp[n][k]; //nilai pulangan
}