Em vez de apenas calcular o hash de uma sequência, podemos armazenar o valor em cada um de seus prefixos. Observe que esses serão valores de hash para sequências iguais ao prefixo correspondente.
Com essa estrutura, você pode calcular rapidamente o valor de hash para qualquer subsegmento dessa sequência (semelhante às somas de prefixos).
Se quisermos calcular o hash do subsegmento [l;r], precisamos pegar o hash no prefixo r e subtrair o hash no prefixo l-1 multiplicado por p à potência de r-l+1. Por que isso acontece fica claro se você escrever os valores nos prefixos e ver o que acontece. Espero que consiga olhar para esta foto.
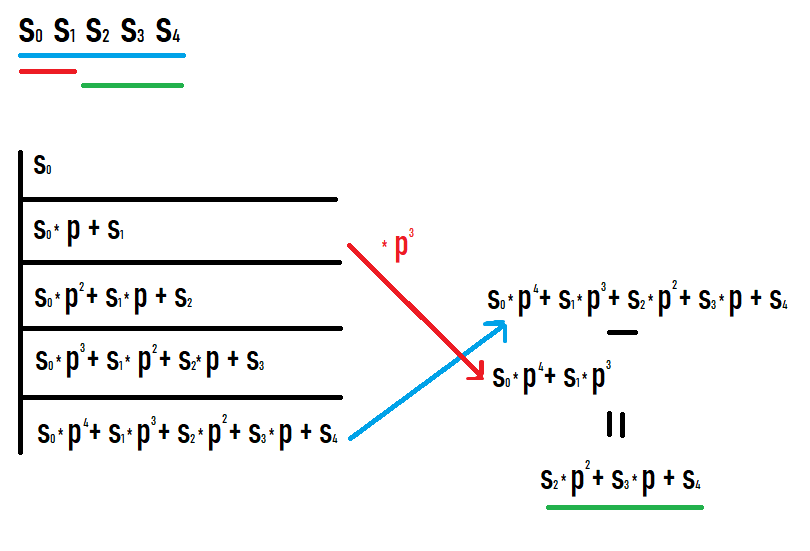
Como resultado de tais ações, obtemos um hash de um subsegmento da sequência original. Além disso, este hash é igual ao que se fosse considerado como um hash de uma sequência igual a este subsegmento (não são necessárias conversões adicionais de graus ou similares para comparar com outros valores).
Há dois pontos a serem esclarecidos aqui:
1) Para multiplicar rapidamente por p à potência r-l+1, é necessário pré-calcular todas as potências possíveis de p módulo mod.
2) Deve-se lembrar que realizamos todos os cálculos módulo módulo e, portanto, pode acontecer que, após subtrair os hashes do prefixo, obteremos um número negativo. Para evitar isso, você sempre pode adicionar mod antes de subtrair. Além disso, não se esqueça de calcular o valor do módulo após as multiplicações e todas as adições.
No código fica assim:
#include <bits/stdc++.h>
usando namespace std;
typedef long longll;
const int MAXN = 1000003;
// módulo base e hash
ll p, mod;
// prefixo hash e expoentes p
h[MAXN], pows[MAXN];
// calculando o hash do subsegmento [l;r]
ll get_segment_hash(int l, int r) {
return (h[r] + mod - h[l - 1] * pows[r - l + 1] % mod) % mod;
}
int main()
{
// de alguma forma obter p e mod
// pré-calcula as potências p
poder[0] = 1;
para (int i = 0; i < MAXN; i++)
pows[i] = (pows[i - 1] * p) % mod;
//
// solução do problema principal
//
retorna 0;
}