Problem
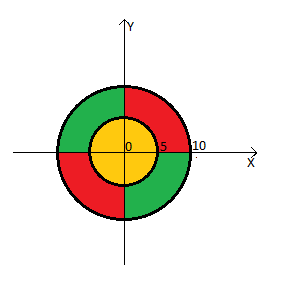
Willy jogou um amistoso contra o Emmy por o título de campeão mundial. Quando se cansaram das longas batalhas de xadrez, mudaram para os dardos. O jogo de dardos era o seguinte: todos lançavam um dardo em um círculo, localizado a vários metros de distância. O círculo tinha uma marcação especial, dividida em várias áreas por círculos de raio 10 e raio 5 (ver figura). Um dardo acertando a área vermelha trazia
20 pontos, acertando o verde -
15 pontos, atingir o amarelo é
30 pontos e atingir o centro é
50 pontos. Se o dardo atingisse a fronteira das regiões, isso daria um número de pontos igual à pontuação máxima das regiões limítrofes.
Um acerto de dardo será codificado condicionalmente por um ponto com a coordenada (
x ,
y). Willy e Emmy fizeram 2 lançamentos com dardos. É preciso calcular qual deles ganhou.
Escreva um programa que contará e exibirá o vencedor desse jogo. Imprima o nome do vencedor (
W - Willie,
E - Emmy) e, separados por um espaço, seus pontos. Se for igual, imprima
W=E e o número de pontos.
Entrada
A entrada é de 4 linhas com 2 números em cada linha (todos os números são inteiros). As duas primeiras linhas são coordenadas dos pontos (
x ,
y) onde os dardos de Willy atingiram (
W), a terceira e quarta linhas - onde os dardos de Emmy atingiram (
E).
Impressão
Imprima o nome do vencedor (W - Willie, E - Emmy) e, separados por um espaço, suas pontuações. Se for igual, imprima W=E e o número de pontos marcados, separados por um espaço.
Exemplos
| # |
Entrada |
Saída |
| 1 |
0 0
-5 7
1 1
5 7 |
W 65 |
| 2 |
0 0
5 5
0 0
5 5 |
W=E 70 |