sub-rotinas. recursão

Um procedimento ou função pode conter uma chamada para outro procedimento dentro dele. Inclusive, a sub-rotina pode chamar a si mesma. Nesse caso, o computador não se importa. Ele também, como sempre, executa consistentemente os comandos que conhece de cima para baixo.

Se você se lembra da matemática, pode encontrar o princípio da indução matemática. É o seguinte:

Uma certa afirmação é verdadeira para todo natural n se
    1. é válido para n = 1 e
    2. da validade da afirmação para qualquer natural arbitrário n = k  segue-se que é verdade para n = k+1.

Na programação, essa técnica é chamada de recursão

Recursão é uma forma de definir um conjunto de objetos em termos do próprio conjunto, com base em casos básicos simples fornecidos.

Recursivo também será chamado de procedimento (função) que chama a si mesmo diretamente ou por meio de outros procedimentos e funções
Exemplo de procedimento recursivo: procedimento Rec(a: inteiro); começar     se um > 0 então         Rec(a - 1);     escreva(a); fim; Esquematicamente, o trabalho de recursão pode ser representado por um fluxograma

 

O procedimento Rec() é executado com o parâmetro 3. Em seguida, dentro do procedimento com o parâmetro 3, é chamado o procedimento com o parâmetro 2, e assim sucessivamente, até que seja chamado o procedimento com o parâmetro 0. Quando o procedimento com o parâmetro parâmetro 0 for chamado, a chamada recursiva já não acontecerá e o procedimento com parâmetro 0 imprimirá o número 0 e terminará. Em seguida, o controle é transferido de volta para o procedimento com o parâmetro 1, ele também termina seu trabalho imprimindo o número 1 e assim por diante. antes do procedimento com o parâmetro 3. 

Todos os procedimentos chamados são armazenados na memória até que concluam seu trabalho. O número de procedimentos simultâneos é chamado de profundidade de recursão.

Vimos que a recursão é a execução repetida de instruções contidas em uma sub-rotina. E isso, por sua vez, é semelhante ao trabalho do ciclo. Existem linguagens de programação nas quais a construção do loop está ausente, por exemplo, Prolog. 
Vamos tentar simular o funcionamento do loop for. 
O loop for contém uma variável de contador de passos. Em uma sub-rotina recursiva, tal variável pode ser passada como um parâmetro. //procedimento LoopImitation() com dois parâmetros //Primeiro parâmetro – contador de passos, segundo parâmetro – número total de passos procedimento LoopImitation(i, n: inteiro); começar     writeln('Olá N', i); // Operador a ser repetido para qualquer valor de i     se eu < n então //Até que o contador de loop se torne igual ao valor n,         LoopImitation(i + 1, n); //chama uma nova instância do procedimento, com o parâmetro i+1 (transição para o próximo valor i) fim;

Iteração na programação — em um sentido amplo — organização do processamento de dados, na qual as ações são repetidas várias vezes, sem levar a chamadas para si mesmas (ao contrário de  %BA%D1%83%D1%80%D1%81%D0%B8%D1%8F" title="Recursão" >Recursões). No sentido estrito — processo de processamento de dados cíclicos em uma etapa. 
Freqüentemente, algoritmos iterativos na etapa atual (iteração) usam o resultado da mesma operação ou ação calculada nas etapas anteriores.  Um exemplo desses cálculos é o cálculo das relações de recorrência. 
Um exemplo simples de valor recursivo é o fatorial: \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\) O cálculo do valor em cada etapa (iteração) é \(N=N \cdot i\) .  Ao calcular o valor de \(N\), tomamos o valor já armazenado \(N\).< br />
O fatorial de um número também pode ser descrito usando a fórmula recorrente:



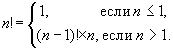
Você pode perceber que esta descrição nada mais é do que uma função recursiva.
Aqui a primeira linha (\(n <= 1\)) — este é o caso base (condição final da recursão) e a segunda linha é a transição para a próxima etapa. 
 

A função fatorial recursiva ficaria assim	Compare o algoritmo para encontrar o fatorial da maneira usual e não recursiva
função Fatorial(n: inteiro): inteiro; começar     se n > 1 então         Fatorial := n * Fatorial(n - 1)     senão         Fatorial := 1; fim;	x := 1; para i := 2 até n faça     x := x * i; writeln(x);

Deve ser entendido que as chamadas de função envolvem alguma sobrecarga adicional, portanto, um cálculo fatorial não recursivo será um pouco mais rápido. 
Conclusão: onde você pode escrever um programa com um algoritmo iterativo simples, sem recursão, então você precisa escrever sem recursão. Ainda assim, existe uma grande classe de problemas onde o processo computacional é implementado apenas por recursão.
Por outro lado, algoritmos recursivos costumam ser mais compreensíveis.