Bir prosedür veya işlev, içindeki başka bir prosedüre çağrı içerebilir. Dahil olmak üzere, alt program kendisini arayabilir. Bu durumda, bilgisayar umursamıyor. Ayrıca, her zaman olduğu gibi, yukarıdan aşağıya tanıştığı komutları tutarlı bir şekilde yürütür.
Matematiği hatırlarsanız, orada matematiksel tümevarım ilkesi ile tanışabilirsiniz. Aşağıdaki gibidir:
bazı ifadeler her doğal n için doğrudur, eğer
1. n = 1 ve için geçerlidir
2. Herhangi bir keyfi doğal n = k için önermenin geçerliliğinden, n = k+1 için doğru olduğu sonucu çıkar.
Programlamada bu tekniğe özyineleme
denir
Yineleme, verilen basit temel durumlara dayalı olarak, bir nesne kümesini kümenin kendisi açısından tanımlamanın bir yoludur.
Tekrarlı kendini doğrudan veya diğer prosedürler ve işlevler aracılığıyla çağıran bir prosedür (işlev) olarak da adlandırılır
Özyinelemeli bir prosedür örneği:
void Rec(int a)
{
eğer (a>0) Rec(a-1);
cout
Şematik olarak, özyineleme işi bir akış şemasıyla temsil edilebilir.
Rec() prosedür parametre 3 ile yürütülür. Ardından, parametre 3 ile prosedür içinde, parametre 2 ile prosedür çağrılır ve parametre 0 ile prosedür çağrılana kadar böyle devam eder. 0 parametresi çağrıldığında, özyinelemeli çağrı zaten gerçekleşmeyecek ve 0 parametresiyle yapılan prosedür 0 sayısını yazdıracak ve sonlandırılacaktır. Daha sonra kontrol 1 parametresi ile prosedüre geri aktarılır, o da 1 sayısını yazdırarak işini bitirir ve bu böyle devam eder. parametre 3 ile prosedürden önce.
Çağrılan tüm prosedürler, işlerini tamamlayana kadar hafızada saklanır. Eşzamanlı prosedürlerin sayısı tekrarlama derinliği olarak adlandırılır.
|
Yineleme. Döngü Simülasyonu
Özyinelemenin, bir alt programda içerilen talimatların tekrar tekrar yürütülmesi olduğunu gördük. Ve bu da döngünün çalışmasına benzer. Döngü yapısının hiç bulunmadığı programlama dilleri vardır, örneğin Prolog.
for döngüsünün çalışmasını simüle etmeye çalışalım.
for döngüsü bir adım sayacı değişkeni içerir. Özyinelemeli bir alt programda, böyle bir değişken parametre olarak iletilebilir.
// İki parametreli LoopImitation() prosedürü.
// İlk parametre – adım sayacı, ikinci parametre – toplam adım sayısı.
geçersiz LoopImitation(int i, int n)
{
cout
|
Yineleme ve yineleme
Yinelemeyi anlamak için yinelemeyi anlamanız gerekir...
Programlamada yineleme döngüsel bir veri işleme sürecinin bir adımı.
Genellikle geçerli adımdaki (yineleme) yinelemeli algoritmalar, önceki adımlarda hesaplanan aynı işlemin veya eylemin sonucunu kullanır. Bu tür hesaplamalara bir örnek, yineleme ilişkilerinin hesaplanmasıdır.
Özyinelemeli değerin basit bir örneği faktöriyeldir: \(N!=1 \cdot 2 \cdot 3 \cdot \ ... \ \cdot N\).
Her adımda (yineleme) değerin hesaplanması şu şekildedir: \(N=N \cdot i\) . \(N\) değerini hesaplarken, önceden depolanmış değeri \(N\) alırız >.
Bir sayının faktöriyeli yinelenen formül kullanılarak da açıklanabilir:
\(\begin{equation*} n!= \begin{cases} 1 &\text{n <= 1,}\\ (n-1)! \cdot n &\text{n > 1.} \end{durumlar} \end{denklem*}\)
Bu açıklamanın özyinelemeli bir işlevden başka bir şey olmadığını fark edebilirsiniz.
Burada ilk satır ( \(n <= 1\)) temel durumdur (yineleme sonlandırma koşulu) ve ikinci satır bir sonraki adıma geçiştir. < br />
| Yinelemeli faktöriyel işlevi |
Yinelemeli algoritma |
|
int Faktöryel(int n)
{
eğer (n > 1)
dönüş n * Faktöriyel(n - 1);
aksi takdirde 1 döndürür;
}
|
x = 1;
için (i = 2; i <= n; i++)
x = x * ben;
cout
|
İşlev çağrılarının bazı ek yük içerdiği anlaşılmalıdır, bu nedenle özyinelemeli olmayan bir faktöriyel hesaplaması biraz daha hızlı olacaktır.
Sonuç: Basit bir yinelemeli algoritmaya sahip, yinelemesiz bir program yazabileceğiniz yerde, yinelemesiz yazmanız gerekir. Ancak yine de, hesaplama sürecinin yalnızca özyineleme ile uygulandığı geniş bir problem sınıfı vardır.
Öte yandan, özyinelemeli algoritmalar genellikle daha anlaşılırdır.
Görev
"Tumba-Yumba" kabilesinin dilinin alfabesinde; dört harf: "K", "L", "M" ve "N". Bu alfabenin harflerinden oluşturulabilen n harflerinden oluşan tüm kelimeleri göstermeniz gerekmektedir.
Sorun, daha küçük bir soruna indirgenebilen normal bir kaba kuvvet sorunudur.
Sözcüğün yerine harfleri sırayla koyacağız.
Bir kelimenin ilk konumu alfabenin 4 harfinden (K. L, M, N) biri olabilir.
Önce K harfini koyalım. Ardından, ilk harf K olan tüm değişkenleri elde etmek için, kalan n - 1 konumlarında tüm olası harf kombinasyonlarını numaralandırmanız gerekir. (resme bakın).
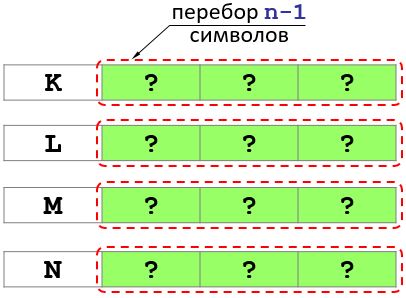 Böylece problem n - 1 uzunluğundaki dört problemi çözmeye indirgenmiştir.
n karakteri tekrarlayarak yinele
w[0]='K'; // son L-1 karakterlerini tekrarla
w[0]='L'; // son L-1 karakterlerini tekrarla
w[0]='M'; // son L-1 karakterlerini tekrarla
w[0]='N'; // son L-1 karakterlerini tekrarla
w - çalışan kelimeyi saklayan bir karakter dizisi.
Böylece özyineleme elde ettik.Problemin çözümünü özyinelemeli bir prosedür şeklinde düzenleyebiliriz.
Özyinelemenin ne zaman sona ereceğini belirlemek için kalır? Tüm karakterler ayarlandığında, yani ayarlanan karakter sayısı n olur. Bu durumda, ortaya çıkan kelimeyi ekranda görüntülemeniz ve prosedürden çıkmanız gerekir.
C++ programı böyle görünecek.
#include<iostream>
ad alanı std kullanarak;
geçersiz TumbaWords( dize A, dize &w, int N )
// w - değiştirilebilir parametre (dize sonucu)
// TumbaWords prosedürü alfabeyi bir karakter dizisi olarak iletir,
// sözcük sözcüğü ve önceden ayarlanmış karakter sayısı (önceki – 0).
{
int ben;
eğer (N == w.size())
{
// tüm karakterler zaten kelimeye ayarlanmışsa,
// o zaman bir dizi çıktısı almak ve prosedürü sonlandırmak gerekir
cout
NOT w değişken bir parametredir (sonuç dizesi)!
|
|