Problem
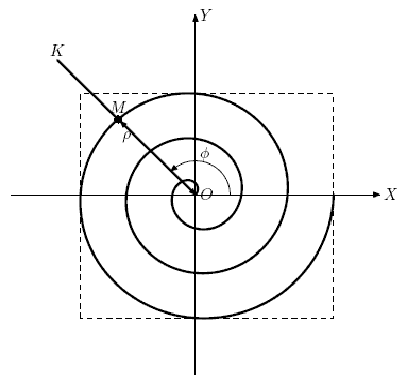
Dima gần đây đã gia nhập Viện nghiên cứu đường cong phẳng. Như tên của viện nghiên cứu này gợi ý, nó tham gia vào nhiều nghiên cứu khác nhau trong lĩnh vực đường cong phẳng. Gần đây, ông chủ của Dimin, Georgy, đã bắt gặp một đường cong rất thú vị, hóa ra sau một số nghiên cứu, nó được gọi là đường xoắn ốc Archimedean. Đường xoắn ốc Archimede là một đường cong phẳng mô tả quỹ đạo của điểm M chuyển động thẳng đều dọc theo tia OK có gốc tọa độ tại O, còn bản thân tia OK quay đều quanh điểm O (xem hình vẽ). Nói cách khác, khoảng cách đến gốc tọa độ ρ = OM phụ thuộc tuyến tính vào góc quay .phi. tia OK. Trong trường hợp này, góc quay của tia OK theo cùng một góc tương ứng với cùng một khoảng cách ρ.
Chuyển động của điểm M có thể được đặt bằng một số tham số:
• góc quay ban đầu .alpha. tia OK (được đo bằng độ ngược chiều kim đồng hồ so với chiều dương của trục OX);
• vận tốc góc .omega. tia OK (được đo bằng độ trên đơn vị thời gian);
• khoảng cách ban đầu R từ điểm M đến gốc tọa độ (điểm O);
• vận tốc V của điểm M dọc theo tia OK.
Nếu, bằng cách đặt các tham số này, chúng ta không giới hạn thời gian chuyển động của điểm M, thì chúng ta sẽ có một đường cong vô hạn, khá khó khám phá. Do đó, Dima quyết định chỉ nghiên cứu một phần của đường cong này, phần thu được khi điểm M di chuyển từ thời điểm 0 đến thời điểm T. Bài toán mà Dima giải quyết là tìm một hình chữ nhật của diện tích nhỏ nhất có các cạnh song song với các trục tọa độ, trong đó nó có thể được ghi.
Bạn cần viết chương trình tìm hình chữ nhật mong muốn
Đầu vào
Tệp đầu vào chứa bốn số nguyên: ω (1 ≤ omega; ≤ 100), V (1 ≤ V ≤ 100), R (0 ≤ R ≤ 100) và T (1 ≤ T ≤ 1000). Trong bài toán này giả sử góc quay ban đầu là .alpha. bằng không.
Đầu ra
Trong dòng đầu tiên của tệp đầu ra, hãy in hai số thực — tọa độ của góc dưới bên trái của hình chữ nhật mong muốn và trong dòng thứ hai — tọa độ của góc trên bên phải của hình chữ nhật mong muốn.
Câu trả lời sẽ được coi là đúng nếu giá trị của mỗi tọa độ khác với giá trị thực không quá 10-5.
| Đầu vào |
Đầu ra |
| 60 10 0 18 |
-150.3028434716 -165.2754877824
180.0000000000 135.3362037333
|
Olympic đồng đội, VKOSHP, 2008, Bài toán I